Overview

Sequences

A sequence is an ordered list of numbers, $a_1, a_2, \dots,$.

Each number in the sequence is called a term of the sequence. We denote sequences in any of the following forms:

$$ \begin{gather} \{a_1, a_2, a_3, \dots, a_n, \dots \}\\ \{a_n\}_{n = 1}^{\infty}\\ \{a_n\} \end{gather} $$

The subscript $n$ that appears in $a_n$ is called an index, and it indicates the order of terms in the sequence. The starting index is arbitrary, but usually $n = 0$ or $n = 1$. The $\dots$ mean that the sequence continues indefinitely.

It is of interest whether a sequence approaches some value for very large values of $n$. A sequence is said to converge if it approaches some value as $n \to \infty$. A sequence is said to diverge if it is unbounded or does not approach any value. The intuition is really what happens to the next term. Is it smaller, bigger, etc.?

Sequence that Converges

The following sequence approaches $n^2/n^2 = 1$:

$$ \begin{gather} a_n = \frac{(n + 8)(n + 1)}{n(n - 10)}\\ = \frac{n^2 + 9n + 8}{n^2 - 10n} \end{gather} $$

Sequences that Diverge

This sequence diverges because the numerator grows much faster than the denominator and so grows unbounded.

$$ b_n = \frac{e^n + 1}{e \cdot n + 1} $$

This sequence is said to diverge because it never approaches any value:

$$ c_n = (-1)^n $$

Instead, it oscillates between $-1$ and $1$,

Types of Sequences

• $\{a_n\}$ is increasing if $a_{n + 1} > a_n$; for example, $\{0, 1, 2, 3, \dots\}$
• $\{a_n\}$ is nondecreasing if $a_{n + 1} \geq a_n$; for example, $\{1, 1, 2, 2, 3, 3, \dots\}$
• $\{a_n\}$ is decreasing if $a_{n + 1} < a_n$; for example, $\{2, 1, 0, -1, \dots\}$
• $\{a_n\}$ is nonincreasing if $a_{n + 1} \leq a_n$; for example, $\{0, -1, -1, -2, -2, -3, -3, \dots\}$
• $\{a_n\}$ is monotonic if it is either nonincreasing or nondecreasing (it moves in one direction).
• $\{a_n\}$ is bounded if there is a number $M$ such that $|a_n| \leq M$, for all relevant values of $n$.

Recurrence Relations

A recurrence relation (or implicit formula) is a way of defining a sequence by providing an initial term, and a general rule from computing the next term from the previous term.

If you have $\{1, 4, 7, 10, \dots \}$, the recurrence relation is:

$$ a_{n + 1} = a_n + 3, a_1 = 1, \text{ for } n = 1, 2, 3, \dots $$

Explicit Formula

An explicit formula we can determine the $n$th term of a sequence directly. An explicit formula is more desirable than a recurrence relation. Here we convert a recurrence relation for ${1, 4, 7, 10, \dots}$ to an explicit formula by first observing a pattern:

$$ \begin{gather} a_1 = 1\\ a_2 = 1 + (3 \cdot 1)\\ a_3 = 1 + (3 \cdot 2)\\ a_4 = 1 + (3 \cdot 3)\\ \end{gather} $$

Observe that the $n$th term of the sequence is $1$ plus $3$ multiplied by $n - 1$, or

$$ \begin{gather} a_n = 1 + 3(n - 1)\\ = 3n - 2, \text{ for } n = 1, 2, 3, \dots \end{gather} $$

Now we can determine $n$th without calculating the previous terms. So, for $n = 147$ we have:

$$ a_{147} = 3 \cdot 147 - 2 = 439 $$

Limit of a Sequence

If the terms of a sequence $\{a_n\}$ approach a unique number $L$ as $n$ increases—that is, if $a_n$ can be made arbitrarily close to $L$ by taking $n$ sufficiently large—then we say $\lim_{n \to \infty} a_n = L$ exists, and the sequence converges to $L$. If the terms of the sequence do not approach a single number as $n$ increases, the sequence has no limit, and the sequence diverges.

Given the sequence:

$$ \left\{ \frac{(-1)^n}{n^2 + 1}\right\}^{\infty}_{n = 1} $$

The first four terms are:

$$ \left\{-\frac{1}{2}, \frac{1}{5}, -\frac{1}{10}, \frac{1}{17}, \dots \right\} $$

The limit appears to be $0$

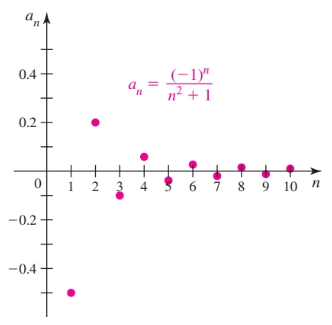
Given the sequence:

$$ \{\cos n \pi \}_{n = 1}^{\infty} $$

The first four terms are:

$$ \{-1, 1, -1, 1, \dots \} $$

The terms of sequence alternate and never approach a single value so this sequence is said to diverge:

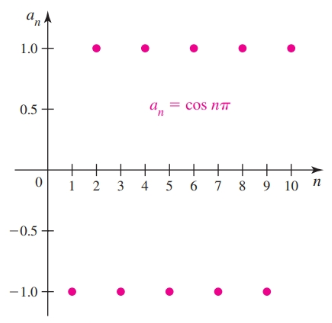
Given the sequence:

$$ \{a_n\}_{n = 1}^{\infty}, a_{n + 1} = -2a_n, a_1 = 1 $$

The first four terms are:

$$ \{1 -2, 4, -8, \dots\} $$

Because the magnitudes of the terms increase without bound, the sequence diverges:

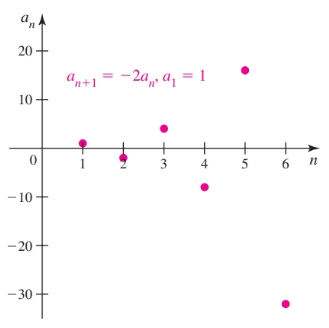
Infinite Series and the Sequence of Partial Sums

An infinite series is a sum of an infinite set of numbers.

Given a sequence $\{a_1, a_2, a_3, \dots \}$, the sum of its terms can be expressed as

$$ a_1 + a_2 + a_3 + \dots = S = \sum_{k = 1}^{\infty} a_k $$

A partial sum of the previous expression is the summing of some subset of the terms starting with $a_1$ e.g.:

$$ S_3 = a_1 + a_2 + a_3 = \sum_{k = 1}^{3} a_k $$

The sequence of partial sums $\{S_n\}$ associated with this series has the terms:

$$ S_n = a_1 + a_2 + a_3 + \dots + a_n = \sum_{k = 1}^n a_k, \text{ for } n = 1, 2, 3, \dots $$

It may be the case that we have some formula for $S_n$ allowing us to find the partial sum for any $n$:

$$ S_n = \frac{n + 1}{n + 10} $$

With this information we can determine any $a_n$. Recall that the sequence of partial sums is:

$$ a_1 + a_2 + a_3 + \dots + a_{n - 1} + a_{n} $$

Observe that it is possible to find the last term $a_n$ with the following equation

$$ a_n = S_n - S_{n - 1} $$

Therefore:

$$ \begin{gather} a_n = \frac{n + 1}{n + 10} - \frac{(n - 1) + 1}{(n - 1) + 10}\\ = \frac{(n + 1)(n + 9)}{(n + 10)(n + 9)} - \frac{n(n + 10)}{(n + 9)(n + 10)}\\ a_n = \frac{9}{(n + 9)(n + 10)} \end{gather} $$

Given the infinite series $S = \sum_{k = 1}^{\infty} a_k = a_1 + a_2 + \dots$ and formula for the $k$th partial sum

$$ S_k = \frac{2k^3}{(k + 1)(k + 2)} $$

Observe that $S$ is the limit of $S_k$ as $k \to \infty$:

$$ S = \lim_{k \to \infty} S_k = \lim_{k \to \infty} \frac{2k^3}{(k + 1)(k + 2)} $$

From here we can determine if the sequence of partial sums i.e. the series diverges or converges.

Given the infinite series:

$$ \sum_{k = 1}^{\infty} \frac{1}{k(k + 1)} $$

we have the following sequences of partial sums:

$$ \begin{gather} S_1 = \frac{1}{2} = \frac{1}{2}\\ S_2 = \frac{1}{2} + \frac{1}{6} = \frac{2}{3}\\ S_3 = \frac{1}{2} + \frac{1}{6} + \frac{1}{12} = \frac{3}{4}\\ S_4 = \frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} = \frac{4}{5}\\ \end{gather} $$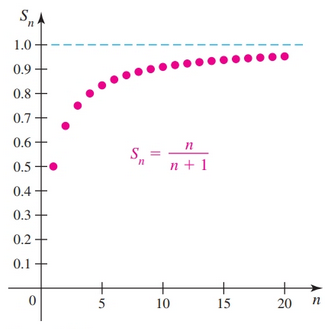

Based on the pattern in the sequence of partial sums, a reasonable conjecture is that $S_n = \frac{n}{n + 1}$, for $n = 1, 2, 3, \dots$, which produces the sequence $\{\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \dots \}$. Because $\lim_{n \to \infty} \frac{n}{n + 1} = 1$, we claim that

$$ \sum_{k = 1}^{\infty} \frac{1}{k(k + 1)} = \lim_{n \to \infty} S_n = 1 $$

Geometric Sequences and Series

Geometric sequences have the property that each term is obtained by multiplying the previous term by a fixed constant, called the ratio. They have the form $\{r^n\}$ or $\{ar^n\}$, where the ratio $r$ and $a$ are real numbers.

$$ \begin{gather} 8 + \frac{8}{3} + \frac{8}{9} + \dots\\ 8 + 8\left(\frac{1}{3}\right) + 8\left(\frac{1}{3}\right)^2 + \dots \end{gather} $$

When $|r| < 1$ the resulting numbers decrease to $0$.

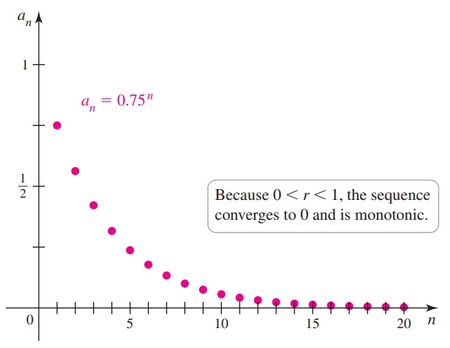
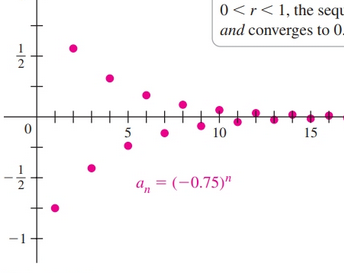
When $-1 < r < 0$, e.g. ${(-0.75)^n}$ the resulting sequence oscillates and converges to $0$.

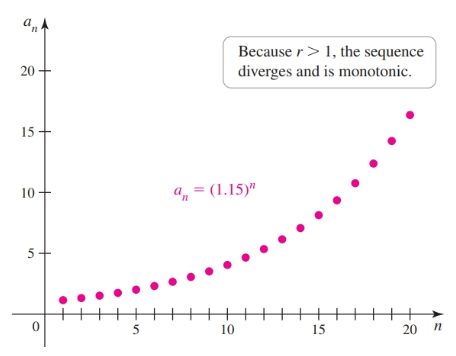
When $r > 1$ then resulting numbers increase in magnitude without bound (diverges).

When $r < -1$ the resulting sequence oscillates and does not converge (diverges).

Geometric Series

Here is the geometric sequence from the beginning expressed as an infinite series:

$$ \sum_{k = 0}^{\infty} 8 \left(\frac{1}{3}\right)^k $$

There are multiple ways to express geometric series.

$$ \sum_{k = 0}^{\infty} ar^k = \sum_{k = 1} ar^{k - 1} = \sum_{k = 5} ar^{k - 5} $$

When $|r| < 1$ we can find the sum of the series with:

$$ \frac{a}{1 - r} $$

Strategies

Given a series such as:

$$ \sum_{j = 1}^{\infty} 8^{-2j} $$

We can refactor:

$$ \begin{gather} 8^{-2j}\\ (8^{-2})^j\\ (8^{-2})(8^{-2})^{j - 1} \end{gather} $$

Given a series such as:

$$ \sum_{k = 1}^{\infty} \frac{3^k}{8^k}\\ $$

We can refactor:

$$ \begin{gather} \frac{3^k}{8^k}\\ \left(\frac{3^k}{8^k}\right)\\ \left(\frac{3}{8}\right)^k\\ \left(\frac{3}{8}\right)\left(\frac{3}{8}\right)^{k - 1}\\ \end{gather} $$

If $k \ne 1, k > 1$, simply find the series, then subtract the missing terms:

$$ \sum_{k = 3}^{\infty} \frac{3}{8}^{k - 1} = \sum_{k = 1}^{\infty} \frac{3}{8}^{k - 1} - \frac{3}{8}^{(3) - 1} - \frac{3}{8}^{(2) - 1} $$

When $k = 0$, our form the series must be:

$$ \sum_{k = 0}^{\infty} -\frac{5}{6}^{k}\\ $$

In this case, $r = -\frac{5}{6}$ and $a = 1$

A rational and repeating number such as $0.161616 \dots$ can be expressed as the sequence:

$$ 0.16 + 0.0016 + 0.000016 + \dots $$

Each term is some ratio ($r$) times the previous number ($.01$). Therefore, this number can be expressed as a geometric series:

$$ \sum_{k = 1}^{\infty} 16 \left(\frac{1}{100}\right)^{k - 1} $$

Telescoping Series

Given a series such as:

$$ \sum_{k = 1}^{\infty} \left( \frac{1}{k} - \frac{1}{k + 1} \right) $$

We can find an explicit formula for the $n$th term of the sequence of partial sums ${S_n}$ by expressing the series in a way that allows it to be collapsed (we cancel out terms):

$$ S_n = \left[ \left( \frac{1}{1} - \frac{1}{2} \right) + \left(\frac{1}{2} - \frac{1}{3}\right) + \dots + \left(\frac{1}{n - 1} - \frac{1}{(n - 1) + 1}\right) + \left(\frac{1}{n} - \frac{1}{n + 1} \right) \right]\\ $$

Observe that the series end at the expression from the original series i.e.:

$$ \left(\frac{1}{n} - \frac{1}{n + 1} \right) $$

And, that we have backtracked from this to an expression that has the first operand as the second operand:

$$ \begin{gather} \left(\frac{1}{n - 1} - \frac{1}{(n - 1) + 1)} \right)\\ = \left(\frac{1}{n - 1} - \frac{1}{n} \right)\\ \end{gather} $$

After cancelling terms we have the expression:

$$ S_n = \left[ \frac{1}{1} - \frac{1}{n + 1} \right]\\ $$

Now, we can find sum for any series given $n$.

Next, we can find find the limit of $S_n$ as $n \to \infty$:

$$ \begin{gather} \lim_{n \to \infty} S_n = \left[ \frac{1}{1} - \frac{1}{\infty + 1} \right]\\ = [ 1 - 0 ]\\ = 1 \end{gather} $$

This tells us that series will eventually converge at $1$.

Strategies

Factor out any large terms:

$$ \begin{gather} \sum_{k = 1}^{\infty} \left( \frac{12}{k} - \frac{12}{k + 1} \right) 12 \sum_{k = 1}^{\infty} \left( \frac{1}{k} - \frac{1}{k + 1} \right) \end{gather} $$

Given a series such as:

$$ \sum_{k = 1}^{\infty} \frac{1}{(k + 5)(k + 6)} $$

Use the method of partial fractions:

$$ \sum_{k = 1}^{\infty} \frac{1}{k + 5} - \frac{1}{k + 6} $$

P-Series and Harmonic Series

A p-series has the general form:

$$ \sum_{k = 1}^{\infty} = \frac{1}{k^p}, p \in \mathbb{R} $$

A p-series converges for $P > 1$, otherwise diverges.

The harmonic series is a P-series:

$$ \sum_{k = 1}^{\infty} = \frac{1}{k}, p \in \mathbb{R} $$

Alternating Series

Alternating series have terms which alternate in sign e.g.:

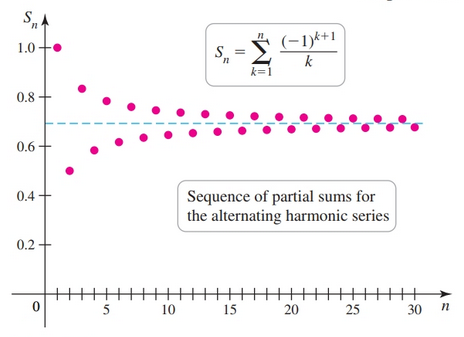
$$ \sum_{k = 1}^{\infty} \frac{(-1)^{k + 1}}{k} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \dots $$

The factor $(-1)^{k + 1}$ has the pattern $\{\dots, 1, -1, 1, -1, \dots \}$, providing the alternating signs.

The alternating harmonic series has the form:

$$ \sum_{k = 1}^{\infty} \frac{(-1)^{k + 1}}{k} $$

Recall that with a regular harmonic series $k > 1$ converges.

It turns out that the alternating harmonic series does converge.

Divergence Test

If the limit as our $k$th term approaches $\infty$ does not equal $0$, then the series diverges. Said another way: if the series does not diverge, then the limit as the $k$th term approaches $\infty$ equals $0$.

Given:

$$ \sum_{k = 1}^{\infty} a_k $$

If

$$ \lim_{k \to \infty} a_k \ne 0 $$

Then the series diverges.

Intuitively, if the limit is not $0$ then we know that the series continues to add numbers and so sum never converges. Observe the conditional nature of the test i.e. if

$$ \lim_{k \to \infty} a_k = 0 $$

Then the test is inconclusive, and other tests are required to determine if the series converges or diverges.

The Integral Test

In order to use the integral test, we make a connection between the infinite series and the integral.

In order use the integral test, the following must be true for $f(k)$:

• is continuous on $[1, \infty)$
• is positive for $x \geq 1$
• decreasing

Given the following series:

$$ \sum_{k = 1}^{\infty} a_k $$

We find the limit of the improper integral for $f(x) = a_k$ to determine whether or not the series convertges. The lower limit is the first value for $k$ and the upper bound is $\infty$:

$$ L = \lim_{b \to \infty} \int_{1}^{b} f(x) dx $$

If $L = \infty$ then the series is divergent; otherwise, the sum converges at $L$.

Ratio Test

Given a series take limit of $a_{k + 1}$ divided by $a_k$ as $k \to \infty$ to find the ratio between the two terms.

$$ r = \lim_{k \to \infty} \frac{a_{k + 1}}{a_k} $$

• If $0 \leq r \lt 1$, the series converges.
• If $r > 1$, the series diverges.
• If $r = 1$, the test is inconclusive.

Strategies

Series containing factorials are particularly amenable to the ratio test:

Comparison Test

Given two series:

$$ \begin{gather} \sum_{n = 1}^{\infty} a_n\\ \sum_{n = 1}^{\infty} b_n \end{gather} $$

and the following conditions for $n = 1, 2, 3, \dots$:

$$ \begin{gather} a_n, b_n \geq 0\\ a_n \leq b_n \end{gather} $$

We can reason that $a_n$ is bounded by $b_n$. Therefore, if $\sum_{n = 1}^{\infty} b_n$ converges, then $\sum_{n = 1}^{\infty} a_n$ also converges.

Contrarily, we can also reason that if $\sum_{n = 1}^{\infty} a_n$ diverges, then $\sum_{n = 1}^{\infty} b_n$ also diverges.

Limit Comparison Test

Given some infinite series $\sum a_k$ we use second related series $\sum b_k$ to determine if $\sum a_k$ converges.

Series $b_k$ is one such that through multiplication, the numerator and denominator in series $a_k$ have the same degree.

More specifically, we are finding the limit of $a_k$ divided by $b_k$

$$ \lim_{k \to \infty} \frac{a_k}{b_k} = L $$

If $0 < L < \infty$, then $\sum a_k$ and $\sum b_k$ either both converge or both diverge.

If $L = 0$ and $\sum b_k$ converges, then $\sum a_k$ converges.

If $L = \infty$ and $\sum b_k$ diverges, then $\sum a_k$ diverges.

Strategies

This test is helpful with series that are expressed in terms of rational functions:

$$ \sum_{k = 1}^{\infty} \frac{1}{4k^{\frac{8}{7}} + 4} $$

In this case, we choose $\sum b_k$ of:

$$ \sum_{k = 1}^{\infty} \frac{1}{k^{\frac{8}{7}}} $$

Which happens to converge.

Finding the limit of $\frac{a_k}{b_k}$, we have:

$$ \begin{gather} \lim_{k \to \infty} \frac{\frac{1}{4k^{\frac{8}{7}} + 4}} {\frac{1}{k^{\frac{8}{7}}}}\\ = \frac{k^{\frac{8}{7}}}{4k^{\frac{8}{7}} + 4} = \frac{1}{4} \end{gather} $$

Since $\sum b_k$ converges and $0 < L < \infty$, $\sum a_k$ converges.

When $a_k$ is a root term take care to choose a $b_k$ that is not under a radical:

$$ \sum_{k = 1}^{\infty} \sqrt{\frac{4k^3}{4k^5 + 7}} $$

Here, we choose $b_k = \frac{1}{k}$.

Some expressions are even tricker:

$$ \sum_{k = 1}^{\infty} \frac{4}{k \sqrt{k + 7}} $$

We can modify $a_k$:

$$ \frac{4}{\sqrt{k^3 + 7k^2}} $$

We choose a $b_k$ of:

$$ \frac{1}{\sqrt{k^3}} $$

Alternating Series Test

Given the alternating series $\sum_{k = 1}^{\infty} a_k, where $a_k = (-1)^k b_k$ or $a_k = (-1)^{k + 1} b_k$ where $b_k \geq 0$ it will converge if:

1. $\lim_{k \to \infty} b_k = 0$

AND

2. The sequence ${b_k}$ is decreasing e.g $1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \dots$

The nature of this test is conditional. We can use it to prove that a series converges, but we cannot use it to prove that a series diverges.

Strategies

Given a sequence we factor out the term that makes the series alternating:

$$ \begin{gather} \sum_{n = 1} \frac{(-1)^{n + 1}}{n}\\ a_n = \frac{(-1)^{n + 1}}{n} = (-1)^{n + 1} \cdot \frac{1}{n}\\ b_n = \frac{1}{n} \end{gather} $$

Now, we can perform the test.

You may not be able to take the absolute value; instead, you will remove the part of the expression that causes series to alternate:

$$ \sum_{k = 1}^{\infty} \frac{\cos \pi k}{k^2} $$

Here, we evaluate the following instead:

$$ \sum_{k = 1}^{\infty} \frac{1}{k^2} $$

Conditional and Absolute Convergence

Given the following series

$$ \sum_{n = 1} \frac{(-1)^{n + 1}}{n} $$

which converges per the alternating series test, we can further classify it based on what happens when we take the absolute value of each term in the sequence:

$$ \sum_{n = 1} \left| \frac{(-1)^{n + 1}}{n} \right| $$

When we take the absolute value of this series we end up with the harmonic series:

$$ \sum_{n = 1} \left| \frac{1}{n} \right| $$

Since this series diverges, we say that the original series converges conditionally. This is an example of conditional convergence.

If on the other hand we end up with a series that converges. The series is an example of absolute convergence.

Alternating Series Remainder

Given the following alternate series:

$$ \sum_{n = 1}^{\infty} \frac{(-1)^{n + 1}}{n^2} $$

We can create an estimate for $S$. First we split our series into a partial sum $S_n$ for some $n$ and $R_n$ for the remainder:

$$ S = \underbrace{1 - \frac{1}{4} + \frac{1}{9} - \frac{1}{16}}_{S^4} + \underbrace{\frac{1}{25} - \frac{1}{36} + \frac{1}{49} - \frac{1}{64} + \dots}_{R_4} $$$$ S = \frac{115}{144} + R_4 $$

Examining $R_4$ we can establish that $R_4 > 0$:

$$ R_4 = \left(\frac{1}{25} - \frac{1}{36}\right) + \left(\frac{1}{49} - \frac{1}{64}\right) + \dots $$

Secondly, we can establish that $R_4 < \frac{1}{25}$:

$$ R_4 = \frac{1}{25} - \left(\frac{1}{36} + \frac{1}{49}\right) - \left(\frac{1}{64} + \frac{1}{81} \right) - \dots $$

Therefore, we can find an upper and lower bound for $S$:

$$ \begin{gather} \frac{115}{144} \lt S \lt \frac{115}{144} + \frac{1}{25}\\ 0.7986\bar{1} < S < 0.8386\bar{1} \end{gather} $$

In our approximation the magnitude of our error is no greater than the first term of our remainder sequence i.e. $\frac{1}{25}$.

Power Series

A power series is an infinite series of the form

$$ \sum_{k = 0}^{\infty} c_k x^k = \underbrace{c_0 + c_1 x + c_2 x^2 + \dots + c_n x^n}_{n\text{degree polynomial}} + \underbrace{c_{n + 1} x^{n + 1} + \dots}_{\text{terms continue}} $$

Or, more generally,

$$ \sum_{k = 0}^{\infty} c_k (x - a)^k = \underbrace{c_0 + c_1 (x - a) + c_2 (x - a)^2 + \dots + c_n (x - a)^n}_{n\text{degree polynomial}} + \underbrace{c_{n + 1} (x - a)^{n + 1} + \dots}_{\text{terms continue}} $$

where the center of the series $a$ and the coefficients $c_k$ are constants. This type of series is called a power series because it consists of powers of $x$ or $(x - a)$.

Viewed another way, a power series is built up from polynomials of increasing degree:

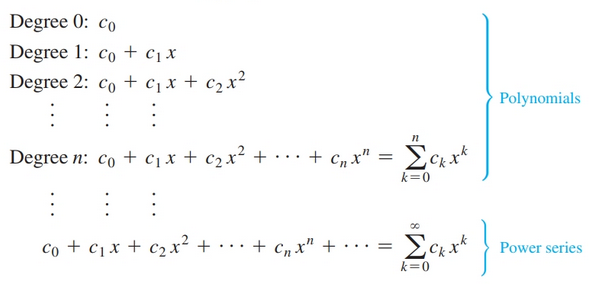
In general power series are use to represent familiar functions such as trigonometric, exponential, and logarithmic functions. They are also used to define new functions. For example, consider the function defined by

$$ g(x) = \sum_{k = 1}^{\infty} \frac{(-1)^k k}{4^k}x^{2k} $$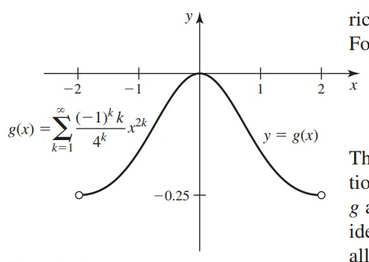

g appears to be an ordinary continuous and differentiable function on 1-2, 22 (which is identified at the end of the chapter). In fact, power series satisfy the defining property of all functions: For each admissible value of x, a power series has at most one value. For this reason, we refer to a power series as a function, although the domain, properties, and identity of the function may need to be discovered.

Convergence and Divergence

Given the power series

$$ \sum_{k = 0}^{\infty} c_k (x - a)^k $$

The set of values of $x$ for which the series converges is its interval of convergence. The radius of convergence of the power series, denoted $R$, is the distance from the center of the series to the boundary of the interval of convergence.

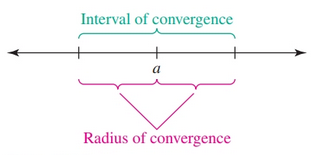
Taylor Polynomials

Given a function $f(x)$ we can approximate it with a polynomial under the following assumptions:

• we can evaluate $f(0)$
• we can evaluate $f'(0), f''(0), f'''(0), f^{(4)}, \dots, f^{(n)}$

Our first estimate $p(x)$ consists of 1 term and must meet the criteria that $p(0) = f(0)$:

$$ p(x) = f(0) $$

This constant function allows for $f(x)$ and $p(x)$ to have the same value at $x = 0$:

• $x = 0, f(0) = p(0)$

Our second estimate $p(x)$ conists of 2 terms; we add to our criteria that $p'(0) = f'(0)$:

$$ p(x) = f(0) + f'(0)x $$

The commonalities include:

• $x = 0$, $f(0) = p(0)$
• $p'(x) = f'(0)$ so $p'(0) = f'(0)$

Our third esimate is:

$$ p(x) = f(0) + f'(0)x + \frac{1}{2}f''(0)x^2 $$

The commonalities now include:

• $x = 0, f(0) = p(0)$
• $p'(x) = f'(0) + f''(0)x$ so $p'(0) = f'(0)$
• $p''(x) = f''(0)$ so $p''(0) = f''(0)$

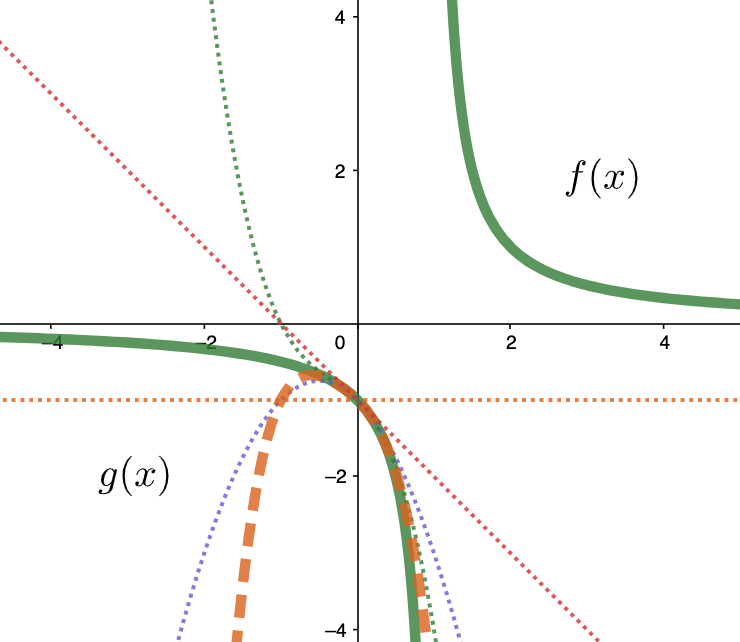
• Observe that each estimate gets better at describing $f(x)$
• $g(x)$ (the thick dashed line) is the most accurate for values near $0$
• the estimates are centered around $0$

We can describe this polynomial that follows this pattern more formally.

Let $f$ be a function with $f', f'', \dots, f^{(n)}$ defined at $a$. The $n$th-order Taylor Polynomial for $f$ with its center at $a$, denoted $p_n$, has the property that it matches $f$ in value, slope, and all derivatives up to the $n$th derivative at $a$; that is,

$$ \begin{gather} p_n(a) = f(a)\\ p_n'(a) = f'(a)\\ \dots\\ p_n^{(n)}(a) = f^{(n)}(a) \end{gather} $$

The $n$th-order Taylor polynomial centered at $a$ is

$$ p_n(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \dots + \frac{f^{(n)}(a)}{n!} (x - a)^n $$

$p_n(x)$ can also written as $p_{n,a} (x)$ to include $a$ on the LHS.

More compactly,

$$ p_n(x) = \sum_{k = 0}^{n} c_k (x - a)^k $$

, where the coefficients are

$$ c_k = \frac{f^{(k)}(a)}{k!}, \text{ for } k = 0, 1, 2, \dots, n $$

If we write the $n$th-order Taylor polynomial for $f$ centered at $a$ and allow $n$ to increase indefinitely, a power series is obtained:

$$ c_0 + c_1(x - a) + c_2(x - a)^2 + \dots + c_n(x - a)^n + \dots = \sum_{k = 0} c_k (x - a)^k $$

This is known as the Taylor series. When a Taylor series is centered at $0$ the series is known as a Maclaurin series.

Taylor Polynomial Remainder

Given a Taylor polynomial $p_n(x)$ that approximates a function $f(x)$ we can describe the amount of error with a remainder/error function $R_{n,a}(x)$ sometimes written as $E_{n,a}(x)$. $p(n)$

$$ R_{n,a}(x) = f(x) - p(x) $$

The error increases the farther we go from $a$. More specifically the error is $0$ up to and including $p_{n,a}^(n)(a)$.

If we have

$$ p_n(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \dots + \frac{f^{(n)}(a)}{n!} (x - a)^n $$

Since

$$ \begin{gather} p(a) = f(a)\\ p'(a) = f'(a)\\ \vdots p^{(n)}(a) = f^{(n)}(a) \end{gather} $$

Then

$$ \begin{gather} R_{n, a}(a) = f(a) - p(a) = 0\\ R_{n, a}'(a) = f'(a) - p'(a) = 0\\ \vdots R_{n, a}^{(n)}(a) = f^{(n)}(a) \end{gather} $$

When we take the $n + 1$th derivative of $p(x)$ we get $0$, so:

$$ \begin{gather} R_{n, a}^{(n + 1)} = f^{(n + 1)}(x) - p^{(n + 1)}(x)\\ = R_{n, a}^{(n + 1)} = f^{(n + 1)}(x) - 0\\ = f^{(n + 1)}(x) \end{gather} $$

Therefore,

$$ |R_{n, a}^{(n + 1)}(x)| = |f^{(n + 1)}(x)| \leq M $$

Sources

• Calculus: Early Transcendentals by Briggs, Cochran, Gillett