Partial Derivatives

Introduction

Consider an equation with multiple variables:

$$ \begin{gather} f(x, y) = x^2y + \sin(y) \end{gather} $$

How do we take the derivative of an equation such as this?

There is a method called the partial derivative which is very similar to ordinary derivatives.

We have ordinary derivatives, e.g.

$$ \begin{gather} \frac{df}{dx} \end{gather} $$

And, recall the interpretation that this is the change in the function for every little change in our variable $x$.

We think of the graphical interpretation regarding slope.

Here is another interpretation where we have two lines, one for $x$ and one for $f$, and a value on one line is mapped to the value on the other line:

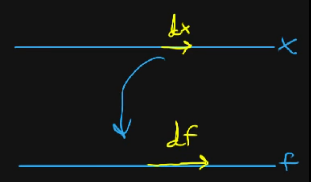
And, we see the change in $x$ corresponding to the change in $f$.

We can pretty much do the same thing in the multivariable world.

However, we use a different notation to emphasize that the equation is multivariable:

$$ \begin{gather} \frac{\partial f}{\partial x} \end{gather} $$

This would be “partial $f$ partial $x$”. It’s partial because it doesn’t really tell the whole story of $f$.

In the case of $\frac{\partial f}{\partial x}$ it doesn’t care about $y$, it treats it as a constant. With our previous expression

$$ \begin{gather} \frac{\partial f}{\partial x}(1, 2) = \frac{\partial}{\partial x}(x^2 \cdot 2 + \sin (2))|_{x = 1}\\ = 4x + 0\\ = 4(1)\\ = 4 \end{gather} $$

For $y$ we have:

$$ \begin{gather} \frac{\partial f}{\partial y}(1, 2) = \frac{\partial}{\partial y}(1 \cdot y + \sin (y))|_{y = 2}\\ = 1 + \cos(2) \end{gather} $$

Obviously, we want a general formula!

Instead of plugging in a constant for the terms we aren’t interested in, we treat them as constants.

So, for $x$ we have:

$$ \begin{gather} \frac{\partial f}{\partial x} = \frac{\partial}{\partial x}(x^2y + \sin(y))\\ = 2xy \end{gather} $$

And, for $y$:

$$ \begin{gather} \frac{\partial f}{\partial y} = \frac{\partial}{\partial y}(x^2y + \sin(y)\\ = x^2 + \cos(y) \end{gather} $$

Sources

• Khan Academy