Parametric Equations
Overview
Imagine that a particle moves along curve $C$:
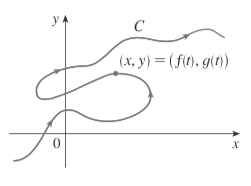
It is impossible to describe $C$ by an equation of the form $y = f(x)$ because $C$ fails the vertical line test. Some curves are best handled when both $x$ and $y$ are given in terms of a third variable $t$, called a parameter. Such equations are called parametric equations. When $t$ is used it may be used to represent time.
The following parametric equations give the position of the particle at time $t$.
$$ \begin{gather} x = f(t), a \leq t \leq b\\ y = g(t) \end{gather} $$Observe that $t$ varies over the interval $[a, b]$.
An important consequence for parametric functions derived from periodic functions is that they can be “retraced” when the interval for $t$ exceeds the period.
Values of the parameter $t$ do not appear in the graph. The only signature of the parameter is the direction in which the curve is generated as indicated by arrows. This is known as the positive orientation.
We can express parametric equations in terms of Cartesian coordinates:
$$ \begin{gather} (x, y) = (f(t), g(t)), \text{ for } a \leq t \leq b \end{gather} $$Graphing Parametric Equations
Given
$$ \begin{gather} x = f(t) = 2t, 0 \leq t \leq 8\\ y = g(t) = \frac{1}{2}t^2 - 4 \end{gather} $$Create a table:
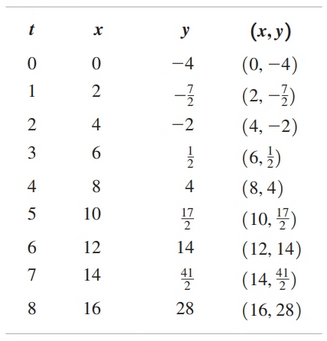
Then plot:
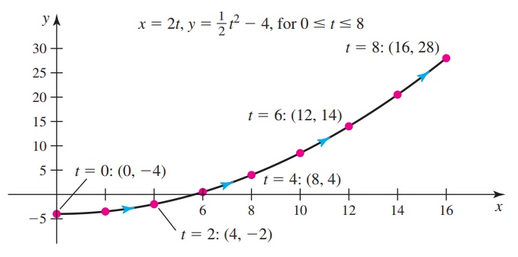
Be sure to indicate direction with arrows.
Converting from Parametric to Cartesian
Sometimes it is possible to eliminate the parameter from a set of parametric equations and obtain a description of the curve in terms of $x$ and $y$. We do this by substituting one equation for $t$ in the other equation.
$$ \begin{gather} y = \frac{1}{2}t^2 - 4, 0 \leq t \leq 8\\ x = 2t\\ \end{gather} $$We solve for $t$:
$$ \begin{gather} \frac{x}{2} = t \end{gather} $$And substitute it back in:
$$ \begin{gather} y = \frac{1}{2} \left(\frac{x}{2}\right)^2 - 4\\ = \frac{x^2}{8} - 4 \end{gather} $$Expressed in this form, we identify the graph as part of a parabola. Because $t$ lies in the interval $0 \leq t \leq 8$ and $x = 2t$, it follows that $x$ lies in the interval $0 \leq x \leq 16$. Therefore, the parametric equations generate the segment of the parabola for $0 \leq x \leq 16$.
Parametric Circle
Parametric equations are also useful for describing circles.
Recall that a circle can be expressed in terms of $x$ and $y$ as:
$$ \begin{gather} x^2 + y^2 = r^2 \end{gather} $$where $r$ is the radius.
It turns at the we can express a circle using parametric equations where one equation is in terms of $\cos$ and the other in terms of $\sin$.
In its simplest form we have an equation that describes a circle of radius $1$:
$$ \begin{gather} \cos(t) + \sin(t) = 1 \end{gather} $$Multiplying both sides by some constant allows for an increased radius:
…
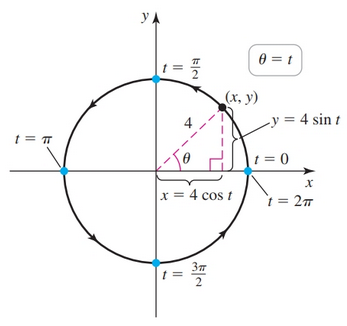
$$ \begin{gather} x = 4 \cos \theta = 4 \cos t, 0 \leq t \leq 2\pi\\ y = 4 \sin \theta = 4 \sin t \end{gather} $$Observe the following:
- the radius of $4$
- the values that $t$ can have
- that $t$ also happens to give a value for $\theta$
- the direction arrow
- when $t = 0$ or $t = 2\pi$ the point is $(4, 0)$
Given the equations:
$$ \begin{gather} x = 4 \cos 2\pi t\\ y = 4 \sin 2\pi t, \text{ for } 0 \leq t \leq 1 \end{gather} $$We plot the following points:
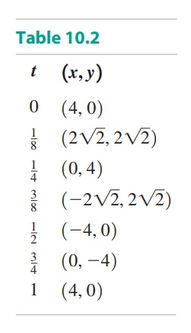
The result is what appears to be a circle of radius $4$ generated with positive orientation in the counterclockwise direction, beginning and ending at $(4, 0)$. Letting $t$ increase beyond $t = 1$ would simply retrace the same curve.

To identify the curve conclusively, the parameter $t$ is eliminated by observing that
$$ \begin{gather} x^2 + y^2 = (4 \cos 2 \pi t)^2 + (4 \sin 2 \pi t)^2\\ = 16\underbrace{(\cos^2 2 \pi t + \sin^2 2 \pi t)}_{1}\\ = 16 \end{gather} $$- Recall the equation of a circle and the trigonometric Pythagorean identity
We can generalize this form to say that for nonzero real numbers $a$ and $b$ equations of the form
$$ \begin{gather} x = \pm a \cos(b t), u \leq t \leq v\\ y = \pm a \sin(b t) \end{gather} $$describe all or part of the circle $x^2 + y^2 = a^2$, centered at the origin with radius $|a|$, for any nonzero value of $b$.
If $b = 1$, then the circle is traversed when $t = 2\pi$. Otherwise, we must find the period
$$ \begin{gather} bt = 2\pi\\ t = \frac{2\pi}{|b|} \end{gather} $$If $t$ represents time, the circle is traversed once in $2 \pi / |b|$ time units, which means we can vary the speed at which the curve unfolds by varying $b$
The constant $|b|$ is called the angular frequency because it is the number of radians the object moves per unit time.
If $b > 0$ then the curve/circle is generated in a counterclockwise direction. If $b < 0$ then the curve/circle is generated in a clockwise direction.
If the circle is not at the origin, and instead at $(x_0, y_0)$, we have the following formula:
$$ \begin{gather} x = x_0 + a \cos b t\\ y = y_0 + a \sin b t \end{gather} $$Our formula for our circle becomes $(x - x_0)^2 + (y - y_0)^2 = r^2$
Parametric Equations of a Line
Recall the point-slope equation for a line:
$$ \begin{gather} y - y_0 = m(x - x_0) \end{gather} $$We can express $x$ and $y$ in terms of $t$ (parametrically) where $\frac{a}{b} = m$ and $-\infty \leq t \leq \infty$.
First isolate $x$ and $y$:
$$ \begin{gather} y - y_0 = \frac{b}{a}(x - x_0)\\ \frac{y - y_0}{b} = \frac{x - x_0}{a} \end{gather} $$Note that when $a = 0$, $\frac{a}{b}$ is undefined i.e. we have a vertical line.
Next, let $t$ equal both sides such that we $t = \frac{x - x_0}{a}$ and $t = \frac{y - y_0}{b}$.
Now, we find the parametric equation for $x$:
$$ \begin{gather} t = \frac{x - x_0}{a}\\ ta = x - x_0\\ x = ta + x_0 \end{gather} $$And, now the parametric equation for $y$:
$$ \begin{gather} t = \frac{y - y_0}{b}\\ tb = y - y_0\\ y = tb + y_0 \end{gather} $$If we need to find the lower and upper limit of $t$ (i.e. you have a line segment) isolate $t$ in the $x$ or $y$ equation:
$$ \begin{gather} x = ta + x_0\\ x - x_0 = ta\\ \frac{x - x_0}{a} = t \end{gather} $$Then plug in the appropriate $x$/$y$ values.
These equations can be used to express a line that passes through $(y_0, x_0)$ with slope $\frac{b}{a}$ with parametric equations.
The following parametric equation can be used to describe a line:
$$ \begin{gather} x = x_0 + at, \text{ for } - \infty < t < \infty\\ y = y_0 + bt \end{gather} $$where $x_0, y_0, a$, and $b$ are constants with $a \ne 0$.
The curve described by these equations is found by eliminating the parameter.
Solving the $x$-equation for $t$ gives u:
$$ \begin{gather} t = \frac{x - x_0}{a} \end{gather} $$When $t$ is substituted into the $y$-equation, the result is a function in point-slope form:
$$ \begin{gather} y = y_0 bt = y_0 + b\left(\frac{x - x_0}{a}\right)\\ y - y_0 = \frac{b}{a}(x - x_0) \end{gather} $$This equation describes a line with slope $\frac{b}{a}$ passing through the point $(x_0, y_0)$
Cycloids
A cycloid is the path of a point on the edge of a rolling wheel.

The exact formula for a cycloid is:
$$ \begin{gather} x = a(t - \sin t), t \geq 0 (a > 0)\\ y = a(1 - \cos t) \end{gather} $$Derivatives of Parametric Curves
Let $x = f(t)$ and $y = g(t)$, where $f$ and $g$ are differentiable on an interval $[a, b]$. Then the slope of the line tangent to the curve (i.e. the derivative) at the point corresponding to $t$ is:
$$ \begin{gather} \frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{g'(t)}{f'(t)} \end{gather} $$provided $f'(t) \ne 0$.
Combined with point $(f(t), g(t))$ and the slope, we can find the equation of the tangent line.
By setting the derivative to $0$ we can find tangent lines of $0$ i.e. where a boundary parallel to the $x$-axis is tangent to the curve.
By setting the derivative to undefined i.e. $\frac{dy/dt}{0}$ we can find vertical lines.
You can find the derivative by solving $f(t)$ for $t$ and then plugging that into $g(t), but such an approach is much more time-consuming.
Second Derivative of $dy/dx$
First, find the first derivative:
$$ \begin{gather} \frac{dy}{dx} = \frac{dy}{dt}/\frac{dx}{dt} \end{gather} $$Then, we have
$$ \begin{gather} \frac{d^2y}{dx^2} = \frac{\frac{d}{dt}\left[\frac{dy}{dx}\right]}{\frac{dx}{dt}} \end{gather} $$Here is one derivation for this:
$$ \begin{gather} \frac{d}{dx}[y] = \frac{\frac{d}{dt}[y]}{\frac{dx}{dt}}\\ \end{gather} $$Now, replace $y$ with $\frac{dy}{dx}$
$$ \begin{gather} \frac{d}{dx}\left[\frac{dy}{dx}\right] = \frac{\frac{d}{dt}\left[\frac{dy}{dx}\right]}{\frac{dx}{dt}}\\ \end{gather} $$If we have the following:
$$ \begin{gather} \frac{dy}{dx} = \frac{1}{2}e^t\\ \frac{dx}{dt} = 6e^{2t} \end{gather} $$Then,
$$ \begin{gather} \frac{d^2y}{dx^2} = \frac{\frac{d}{dt}\left[\frac{dy}{dx}\right]}{\frac{dx}{dt}} = \frac{\frac{1}{2}e^t}{6e^{2t}}\\ = \frac{1}{12e^t} \end{gather} $$Sources
- Calculus: Early Transcendentals by Briggs, Cochran, Gillett