Differential Equations
Overview
A differential equation involves an unknown function and its derivatives. The unknown in a differential equation is not a number but a function.
The highest order differentiation of the unknown function involved in the equation is called the order of the equation.
The following equation is third order since it has a third derivative:
$$ x^2y''' - 4x^5y'' + 7y = 4x^3 $$An ordinary differential equation is a differential equation whose unknown function depends on one real variable e.g.:
$$ x'' + x = \sin t $$So, an ordinary differential equation of order $n$ is an equation involving an unknown function $y$ along with its derivatives:
$$ \frac{dy}{dx}, \frac{d^2y}{dx^2}, \dots, \frac{d^ny}{dx^n} $$More formally, we can express this as:
$$ F \left(x, y, \frac{dy}{dx}, \frac{d^2y}{dx^2}, \dots, \frac{d^ny}{dx^n} \right) = 0 $$There is yet another way to express differential equations.
First order differential equation:
$$ \frac{dy}{dt} = f(t, y) $$Second order differential equation:
$$ \frac{d^2y}{dt^2} = f(t, y, \frac{dy}{dt}) $$And, so on…
A differential equation whose unknown function depends on two, or more, real independent variables is called a partial differential equation.
$$ \frac{d^3u}{dx^2dy} + \frac{du}{dy} = 0 $$A system of differential equations consists of two or more unknown functions. The Lotka-Volterra, or predator-prey, equations are used in ecological modeling:
$$ dx/dt = ax - \alpha x y\\ dy/dt = -cy + \gamma x y $$where $x(t)$ and $y(t)$ are the respective populations of the prey and predator species.
We have solved a differential equation when all the derivatives have been eliminated from the equation and you have expressed the dependent variable, e.g. $y$, in terms of the independent variable, e.g. $x$.
Given the ordinary differential equation:
$$ y'' - 3y' - 4y = 0 $$We can show that any function of the form $y = Ce^{4t}$, where $C$ is a constant, is a solution:
$$ \frac{d^2y}{dx^2} \left(Ce^{4t}\right) - 3 \frac{dy}{dx} \left(Ce^{4t}\right) - 4e^{4t} = 0\\ 16Ce^{4t} - 3(4Ce^{4t}) - 4Ce^{4t} = 0 $$Solutions may also be implicitly defined functions:
$$ xy = \ln y + C $$Is a solution to:
$$ \frac{dy}{dx} = \frac{y^2}{1 - xy} $$Some differential equations have infinitely many solutions, some have no solutions, and others just one.
We assume that is always possible to solve a given ordinary differential equation for the highest derivative, obtaining:
$$ y^{(n)} = f(t, y, y', y'', \dots, y^{(n - 1)}) $$A particular solution of a differential equation is any one solution. The general solution of a differential equation is the set of all solutions.
From the example above, the following are also solutions:
$$ y = \frac{1}{3}e^{4t}\\ y = -2600e^{4t} $$The general solution of a differential equation cannot always be expressed by a single formula. The following equation has two particular solutions $y = 1/x$ and $y \equiv 0$:
$$ y' + y^2 = 0 $$A differential equation along with conditions on the unknown function and its derivatives, all given at the same value of the independent variable, constitutes an initial-value problem. The conditions are known as the initial conditions.
$$ y'' + 2y' = e^x, y(\pi) = 1, y'(\pi) = 2 $$If conditions are given at more than one value of the independent variable, the problem is a boundary-value problem and the conditions are boundary conditions.
$$ y'' + 2y' = e^x, y(0) = 1, y(1) = 1 $$A solution to an initial-value or boundary-value problem is a function that both solves the differential equation and satisfies all given conditions.
Linear Differential Equations
Linear differential equations have the form:
$$ f_0(x) y^{(n)} + f_1(x) y^{(n - 1)} + \dots + f_n(x)y = g(t) $$Observe that all left-hand side coefficients are a function of $x$. Also, a linear differential equation cannot have terms such as $y^2$, $yy'$, or $\sin y$, where $y$ is the unknown function. Equations with such terms are said to be nonlinear and are more complicated to work with. However, some nonlinear equations can be approximated with linearization.
Separation of Variables
An ordinary differential equation is separable if it is possible, by elementary algebraic manipulation, to arrange the equation so that all the dependent variables are on one side and all the independent variables are on the other side.
For example:
$$ \frac{dy}{dx} = 2xy $$Can be rearranged as:
$$ \frac{dy}{y} = 2x dx $$From here, we can integrate both sides (with the constant of integration combined on one side):
$$ \int \frac{dy}{y} = \int 2x dx\\ ln y = x^2 + C\\ e^{\ln y} = e^{x^2 + C}\\ y = e^{x^2 + C} $$Not all ordinary differential equations are separable, e.g.:
$$ x^2y + y^2x = \sin(xy) $$First-Order Linear Equations
First order linear equations of the form have a general solution:
$$ y'(t) = ky + b $$The general solution is derived to be:
$$ y'(t) = ky + b\\ \frac{dy}{dt} = ky + b\\ \frac{dy}{dt} \cdot \frac{1}{ky + b} = 1\\ \int \frac{dy}{dt} \cdot \frac{1}{ky + b} dt = \int dt\\ \int \frac{dy}{ky + b} = \dots\\ \frac{1}{k} \ln |ky + b| = t + C\\ \ln |ky + b| = tk + Ck\\ \ln (ky + b) = tk + C\\ e^{\ln (ky + b)} = e^{tk + C}\\ ky + b = e^C \cdot e^{tk}\\ \dots = Ce^{tk}\\ ky = Ce^{tk} - b\\ y = \frac{C}{k}e^{tk} - \frac{b}{k}\\ y = Ce^{tk} - \frac{b}{k} $$Where $k$ and $b$ are real numbers, and $C$ is an arbitrary constant. Note the reversal of the sign.
Using an Integrating Factor
There is a second way to solve first order linear equations. Given a first order linear equation of the form:
$$ y' + a(x)y = b(x) $$- Note that the RHS is a function of $x$, and all $y$ terms are on the left
We can solve by multiplying both sides by $e$ to the power of the integral of the coefficient on $y$. This known as the integrating factor:
$$ e^{\int a(x) dx} $$Thus, we have:
$$ e^{\int a(x) dx} [y' + a(x)y] = e^{\int a(x) dx} b(x) $$It turns out that:
$$ e^{\int a(x) dx}[ y'(x) + a(x)y] = \frac{d}{dx}[e^{\int a(x) dx} \cdot y] $$So our equation becomes:
$$ \frac{d}{dx}[e^{\int a(x) dx} y] = b(x) \cdot e^{\int a(x) dx} $$Now, we integrate both sides:
$$ \int \left[ \frac{d}{dx}[e^{\int a(x) dx} y] \right] dx = \int [b(x) \cdot e^{\int a(x) dx}] dx\\ e^{\int a(x) dx} y = F(x) + C_1\\ y = \frac{F(x) + C_1}{e^{\int a(x) dx}} $$Ideally, we end with an equation of the form:
$$ y = Ce^{xk} - \frac{b}{k} $$Strategies
Some equations must be modified prior to finding the integrating factor:
$$ x^2 y' + xy = x^2 \cdot \sin x\\ y' + \frac{1}{x} = \sin x $$Given a derivation such as:
$$ \ln |y| = 2x + C $$We can make both sides powers of $e$:
$$ e^{\ln |y|} = e^{x^2 2x + C}\\ |y| = e^C \cdot e^{x^2 + 2x}\\ y = \pm Ce^{x^2 + 2x}\\ y = Ce^{x^2 + 2x} $$You may end up with a derivation such as the following:
$$ y^2 = \frac{6t^3}{5} + C\\ y = \pm \sqrt{\frac{6t^3}{5} + C} $$Note the $\pm$ and the constant inside the square root.
Direction Fields
Consider the first-order differential equation $'y(t) = F(t, y)$, where $F$ is a given expression involving $t$ and/or $y$. A solution of this equation has the property that at each point $(t, y)$ of the solution curve, the slope of the curve is $F(t, y)$. A direction field is simply a picure that shows the slope of the solution at selected points.
Given the equation $y'(t) = y^2e^{-t}$ we choose a regular grid of points in the $ty$-plane, and at each point $(t, y)$, we make a small line segment with slope $y^2e^{-t}$ . The line segment at a point $P$ gives the slope of the solution curve that passes through $P$.
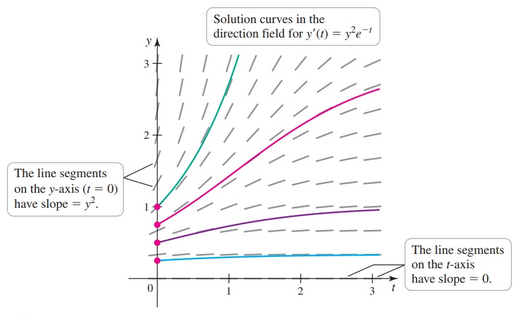
Given initial condition $y(a) = A$ we can start the point $(a, A)$ in the direction field sketch a curve in the positive $t$-direction that follows the flow of the direction field.
Sources
- Calculus: Early Transcendentals by Briggs, Cochran, Gillett