Conic Sections
Overview
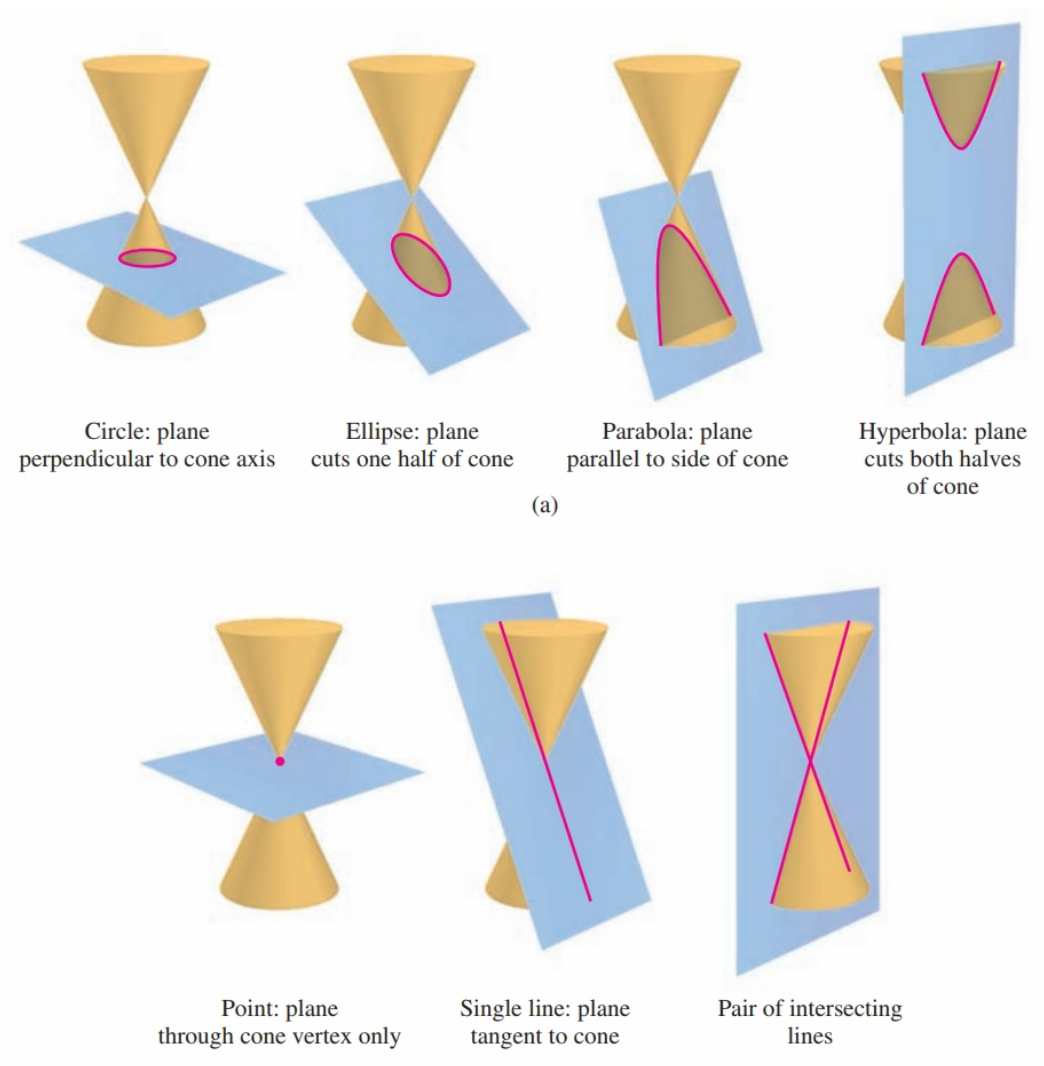
Parabolas
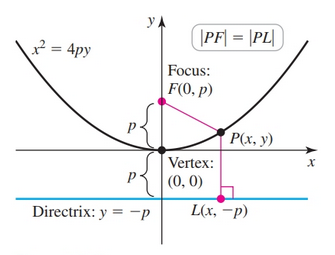
A parabola is the set of points in a plane that are equidistant from a fixed point $F$ (called the focus) and a fixed line (called the directrix). In the four standard orientations, a parabola may open upward, downward, to the right, or to the left.
A parabola is a curved line. For any given point on the parabola, the distance between that point and the directrix is the same as the distance between that point and the focus. The vertex is the point on the parabola closest to the directrix
Vertical

Opens upward if $c > 0$, downward if $c < 0$
- Vertex: $(h, k)$
- Focus: $(h, k + c)$
- Directrix: $y = k - c$
Horizontal

Opens rightward if $c > 0$, leftward if $c < 0$
- Vertex: $(h, k)$
- Focus: $(h + c, k)$
- Directrix: $x = h - c$
Ellipses
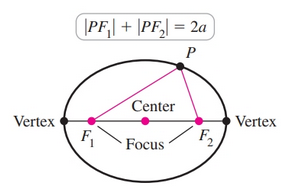
An ellipse is the set of points in a plane whose distances from two fixed points hava constant sum. Each of the two fixed points is a focus (plural foci).
The major-axis of the ellipse is longer axis, while the minor axis is the shorter axis.
For ellipses, there is a diagonal $a$ which is the distance from the point where the minor-axis intercepts the curve with distance $b$ from the center to a focus with distance $c$ from the center. The relationship between the three quantities is expressed in the following way:
$$ a^2 = b^2 + c^2 $$- Observe that $a^2$ is the largest term, and thus determines whether the ellipse is horizontal or vertical.
Horizontal
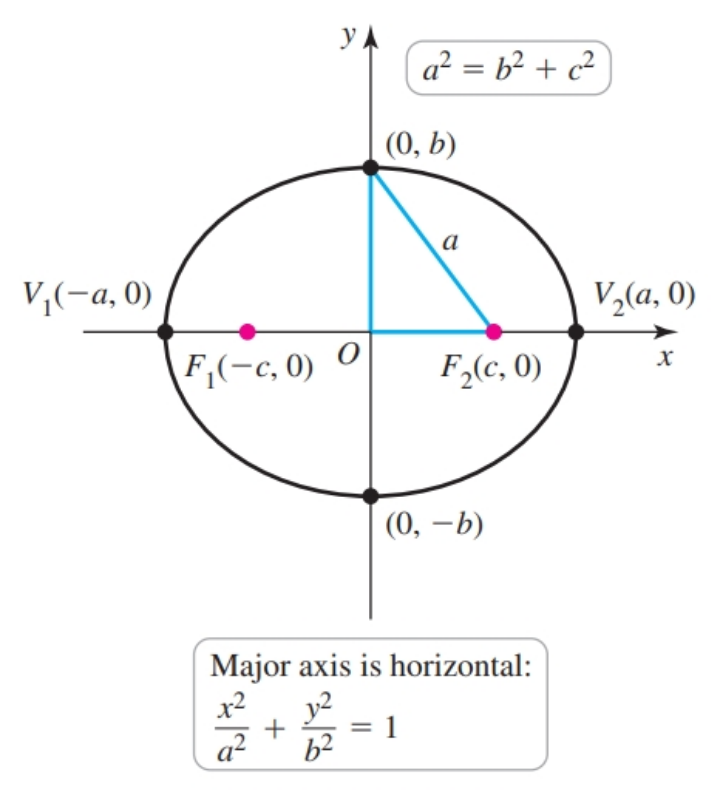
- Center: $(h, k)$
- Vertices: $(h - a, k)$ and $(h + a, k)$
- Foci: $(h - c, k)$ and $(h + c, k)$
- Minor axis endpoints: $(h, k - b)$ and $(h, k + b)$
Vertical
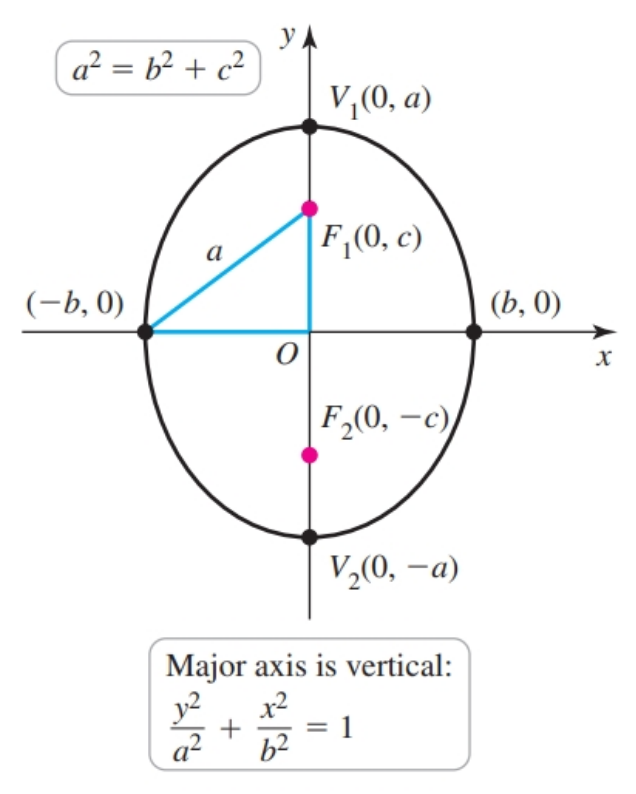
- Center: $(h, k)$
- Vertices: $(h, k - a)$ and $(h, k + a)$
- Foci: $(h, k - c)$ and $(h, k + c)$
- Minor axis endpoints: $(h - b, k)$ and $(h + b, k)$
Hyperbolas
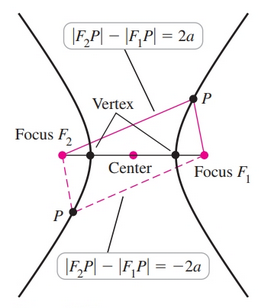
A hyperbola is the set of points in a plane whose distances from two fixed points have a constant difference. The two fixed points are called foci.
For hyperbolas there is a quantity $b$ that is related the distance of the foci from the center $c$ and the distance of the vertices from the center $a$. The relationship is expressed below:
$$ b^2 = c^2 - a^2 $$- Observe that $a^2$ is the largest term, and thus determines whether the ellipse is horizontal or vertical. Also, the order of the terms in the equation matter.
Center: $(h, k)$
Horizontal
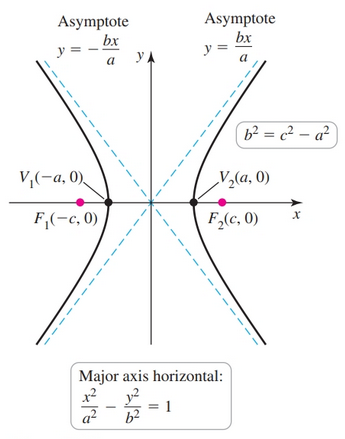
- Vertices: $(h - a, k)$ and $(h + a, k)$
- Foci: $(h - c, k)$ and $(h + c, k)$
- Asymptotes: $(y - k) = \pm \frac{b}{a}(x - h)$
Vertical
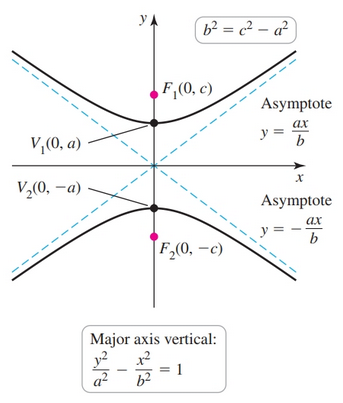
- Vertices: $(h, k - a)$ and $(h, k + a)$
- Foci: $(h, k - c)$ and $(h, k + c)$
- Asymptotes: $(y - k) = \pm \frac{a}{b}(x - h)$
Eccentricity and Directrix
Parabolas, ellipses, and hyperbolas may also be described in a single unified way called the eccentricity-directrix approach. We let $l$ be a line called the directrix and $F$ be a point not on $l$ called the focus. The eccentricity is a real number $e > 0$. Consider the set $C$ of points $P$ in a plane with the property that the distance $|PF|$ equals $e$ multiplied by the perpendicular distance $|PL|$ from $P$ to $l$:
$$ |PF| = e|PL| $$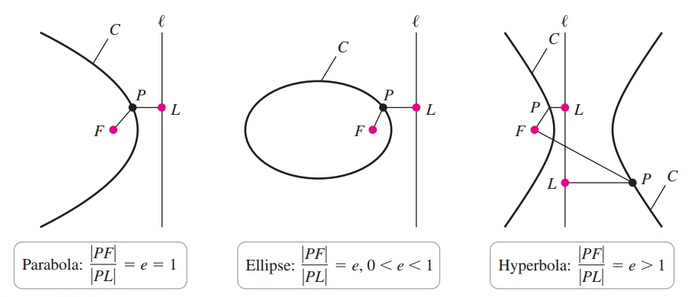
- If $0 < e < 1$, the conic is an ellipse.
- If $e = 1$, the conic is a parabola.
- If $e > 1$, the conic is a hyperbola.
We derive the following equations:
If the directrix/ces is horizontal, then we have:
$$ r = \frac{ed}{1 \pm e \sin \theta} $$If the directrix/ces is vertical, then we have:
$$ r = \frac{ed}{1 \pm e \cos \theta} $$$d$ is the directrix
We can find the vertices by plugging in the appropriate values for $r$.
If the graph uses a $\sin \theta$ function then the vertices are at $6$ o’clock and $12$ o’clock, use $r(\frac{3\pi}{2})$ and $r(\frac{\pi}{2})$. If the graph uses a $\cos \theta$ function then the vertices are at $3$ o’clock and $9$ o’clock, use $r(\pi)$ and $r(0)$. Recall that you can use the appropriate $x = r \sin \theta, y = r \sin \theta$ to find the $x$- and $y$-values.
Note that these are polar coordinates.
The center is halfway between the vertices.
Using the distance between $d$ and the center, we can find the second directrix.
One focus is at $(0, 0)$. If the graph is a hyperbola or an ellipse, then there is another focus which is the same distance from the center as the focus at $(0, 0)$
Only hyperbolas have asymptotes.
Strategies
Ideally, we want an equation such that the denominator is of the form $1 \pm e t(\theta)$ where $t(\theta)$ is $\cos \theta$ or $\sin \theta$ and $e$ is a constant that represents eccentricity. Note that the first operand is $1$ and the second operand is a trig function. It may be the case that we need to factor some number to get to this form:
$$ 3 + \cos \theta\\ = 3(1 + \frac{1}{3} \cos \theta)\\ = \frac{1/3}{1/3} \cdot 3(1 + \frac{1}{3} \cos \theta)\\ $$The denominator is the product of the directrix and the eccentricity. So, for a given equation such as:
$$ r = \frac{3}{1 + \frac{1}{3} \cos \theta} $$We need only divide the numerator by the coefficient on the trig function to express the equation such that the numerator is $de$:
$$ r = \frac{9 \cdot \frac{1}{3}}{(1 + \frac{1}{3} \cos \theta)} $$Given vertices and a directrix we can find eccentricity. Since have a focus at $(0, 0)$ our distance to our first point is $|PF|$. Recall that $|PL|$ is the distance between that same point on the graph (the chosen vertex) and the directrix. Now, we can set up the equation to solve for $e$:
$$ \frac{|PF|}{|PL|} = e $$You may need find an equation after being given values for the vertices, directrix, and $e$. Pay close attention to the signs. If you have a directrix of $y = -2$ and $e = 4$ and are plugging these values in for:
$$ r = \frac{de}{1 - e\sin\theta} $$It is implied that the product in the numerator is positive. So, we will have:
$$ r = \frac{8}{1 - 4 \sin \theta} $$Sources
- Calculus: Early Transcendentals by Briggs, Cochran, Gillett