Polynomials
Quadratic Equations
Overview
A parabola is a symmetric curve that curve upward or downard.
- The vertex is the maximum or minimum point of a parabola described by $x$ and $y$ coordinates
- The axis of symmetry runs through the vertex of a parabola and is described by an $x$ value.
- The y-intercept describes where the parabola intersects the $y$-axis (once).
- The x-intercept describes where the parabola intersects the $x$-axis (twice, once, or no times). The $x$-intercepts are equidistant to the axis of symmetry and the vertex.
- a parabola that opens upward has upward concavity
Equations that describe parabolas involve second-degree terms.
The simplest parabola is $y = x^{2}$.
$y = 2x^{2} - 5x + 7$ is a more complex example.
These equations are generally called quadratics, and are represented, generally, by parabolas.

The same quadratic equation can be expressed four different ways:
Quadratic in factored form
$$ \begin{align} y = 3(x - 1)(x + 5) \end{align} $$- note that there is no second degree term
Vertex form
$$ \begin{align} y = 3(x + 2)^{2} - 27 \end{align} $$- note that there is no first degree term
- in vertex form the non-second-degree term is the $y$-intercept
Standard form
$$ \begin{align} y = 3x^{2} + 12x - 15 \end{align} $$- we may derive the quadratic formula from standard form, and subsequently determine the vertex, and the number of $x$-intercepts
Quadratic formula
This formula is derived from an equation of the form $ax^{2} + bx + c$ i.e. an equation in standard form.
$$ \begin{align} x = \frac{-12 \pm \sqrt{12^{2} - 4(2)(-15)}}{2(-15)} \end{align} $$- The equation is modified such that $x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$
- the $x$-coordinate for the vertex can be found with a component of the quadratic formula $\frac{-b}{2a}$
- The term $\sqrt{b^{2} - 4ac}$ is known as the discriminant. A negative discriminant means that parabola does not intersect the $x$-axis, a positive discriminant means that the parabola intersects the $x$-axis twice, and a discriminant of $0$ means that the parabola intersects the $x$-axis once.
Other notes
- a negative sign on the 2nd degree term indicates a parabola that opens downward (downward concavity); a positive sign indicates the opposite
Problems related to quadratics:
- graphing a quadratic equation
- identifying the vertex
- determining attributes of a parabola
- converting a quadratic equation from one form to another
- solving for $x$ such that $f(x) = 0$ ($x$-intercepts)
- transforming a parabola (upward/downward, larger/smaller, etc.)
Parabolas have $0$, $1$, or $2$ $x$-intercepts:
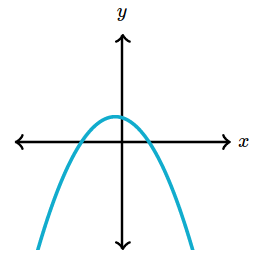

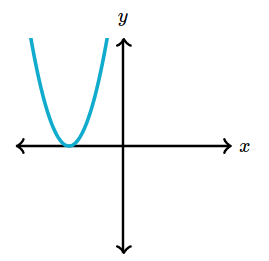
Area Model of Quadratics
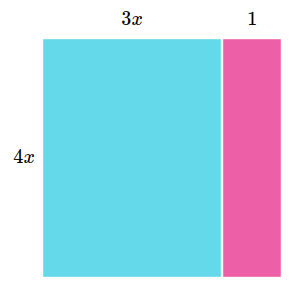
A rectangle with a height of $4x$ and width of $3x + 1$ has an area of $4x \times (3x + 1)$:
A rectangle with a height of $5$ and a width of $4x^2 - 2x - 6$:

Given rectangle whose height is $x + 2$ and width is $x + 3$, we can divide into $4$ rectangles:
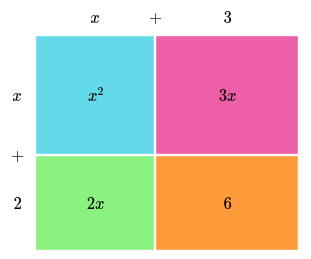
Now are can be expressed as the sum of the $4$ rectangles $x^2 +3x + 2x + 6$.
The square below has an area of $16+8x+x^2$ square meters.
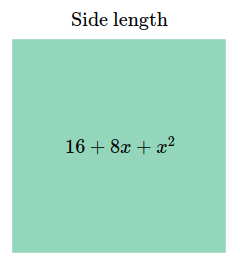
The sides are $(x + 4)$ meters long.
Binomial Special Products
These types of binomial multiplication problems come up time and time again, so it’s good to be familiar with some basic patterns. The “difference of squares” pattern:
$$ \begin{gather} (a+b)(a-b)=a^2-b^2 \end{gather} $$Two other patterns:
$$ \begin{gather} \begin{aligned} &(a+b)^2=a^2+2ab+b^2\\\\ &(a-b)^2=a^2-2ab+b^2 \end{aligned} \end{gather} $$Solving Quadratics
By solving quadratics we mean finding the $x$-intercepts for a given quadratic equation.
The Zero Product Property
Given the equation in factored form:
$$ \begin{align} f(x) = (2x - 1)(x + 5) \end{align} $$First assign $y$ to $0$ since the parabola intersects the $x$-axis when the $y$ value is $0$:
$$ \begin{align} (2x - 1)(x + 5) = 0 \end{align} $$The zero product property states that if $a \cdot b = 0$ then either $a$ or $b$ is equal to $0$.
$$ \begin{align} 2x - 1 = 0 \\ 2x = 1 \\ x = \frac{1}{2} \end{align} $$Or
$$ \begin{align} x + 4 = 0 \\ x = -4 \end{align} $$In an equation like this you can actually have two solutions indicating the parabola intersects the $x$-axis at two points.
Solving quadratics by taking square roots (example)
Given the equation in vertex form what are the $x$-intercepts?
$$ \begin{align} 2x^{2} + 3 = 75\\ 2x^{2} = 72\\ x^{2} = 36\\ x = \pm 6 \end{align} $$Solving quadratics by factoring (example)
Given the equation in standard form what are the $x$-intercepts?
$$ \begin{align} s^{2} - 2s - 35 = 0\\ \end{align} $$First, factor:
$$ \begin{align} (s - 7)(s + 5) = 0 \end{align} $$Then find two instances where the equation can be satisfied:
$$ \begin{align} s = 7 \text{and} s = -5 \end{align} $$Solving quadratics by factoring (leading coefficient $\ne 1$)
Given the equation in standard form what are the $x$-intercepts?
$$ \begin{align} 6x^{2} - 120x + 600 = 0\\ 6(x^{2} - 20x + 100) = 0\\ (x - 10)^{2} = 0\\ \end{align} $$Since there is only one value for $x$ which satisfies this equation, we know that $x$ is $10$
Note that $6(x^{2} - 20x + 100)$ and $(x - 10)^{2}$ intersect the $x$-axis at the same point, but they are not the same parabola—as shown below:
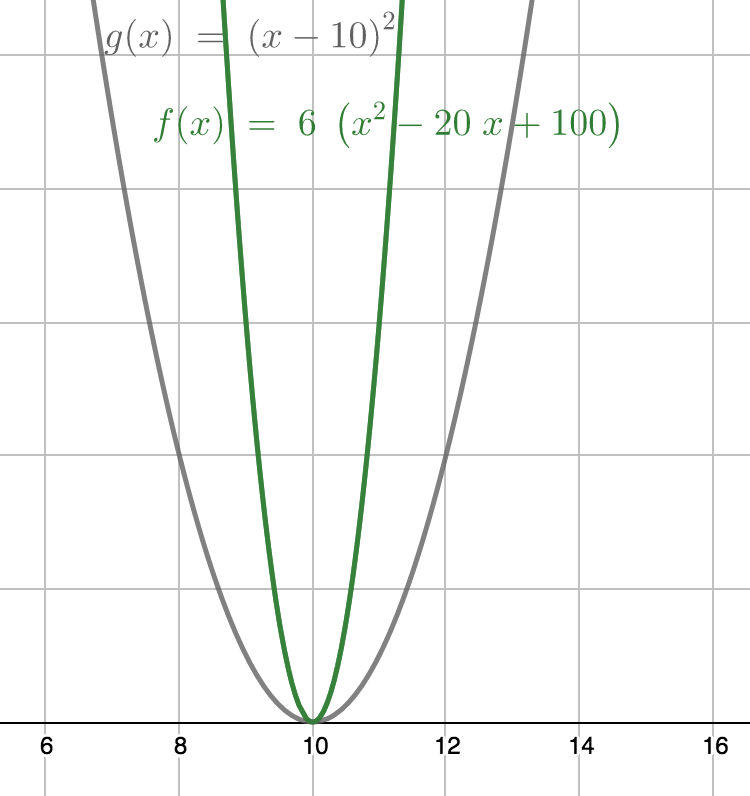
This is the case when any coefficient is factored out…
Solving quadratics using structure
Solve:
$$ \begin{align} (2x - 3)^{2} = 4x - 6\\ (2x - 3)(2x - 3) = 2(2x - 3)\\ \end{align} $$We will now substitute in $p$ for $(2x - 3)$:
$$ \begin{align} p^{2} = 2p\\ p^{2} - 2p = 0\\ p(p - 2) = 0\\ p = 0 \text{and} p = 2 \end{align} $$Next, we’ll substitute $p$ back into the original equation:
$$ \begin{align} 2x - 3 = 0\\ 2x = 3\\ x = \frac{2}{3}\\ \text{or}\\ 2x - 3 = 2\\ 2x = 5\\ x = \frac{5}{2} \end{align} $$Solving quadratic by completing the square
Given an equation close to standard form we can find the $x$-intercepts using completing the square:
$$ \begin{align} x^{2} + 6x = -2 \end{align} $$First, rearrange the equation to standard form:
$$ \begin{align} x^{2} + 6x + 2 = 0 \end{align} $$Then complete the square for the first and second terms:
$$ \begin{align} x^{2} + 6x + 9 + 2 - 9 = 0 \end{align} $$We completed the square by diving $6$ by $2$ and squaring it such that part of the equation can be factored to a perfect square. Since we are adding $9$ we must also subtract $9$ to keep the equation balanced.
$$ \begin{align} (x + 3)^{2} 2 - 9 = 0\\ (x + 3)^{2} - 7 = 0\\ (x + 3)^{2} = 7\\ x + 3 = \pm \sqrt{7} x = \pm \sqrt{7} - 3 \end{align} $$Solving quadratic by completing the square (leading coefficient $\ne 1$
Given the following equation in standard form find the $x$-intercepts:
$$ \begin{align} y = 4x^{2} + 40x + 280 \end{align} $$First, assign $y$ to $0$:
$$ \begin{align} 0 = 4x^{2} + 40x + 280 \end{align} $$In order to complete the square we need the coefficient of the second degree term to be $1$ so we factor out the $4$:
$$ \begin{align} 0 = 4(x^{2} + 10x + 70)\\ 0 = x^{2} + 10x + 70\\ 0 = x^{2} + 10x + 25 + 70 - 25\\ 0 = (x + 5)^{2} + 45\\ -45 = (x + 5)^{2} \end{align} $$Now, you can see that there can be no solution as you cannot unsquare a negative number. If we assume $x$ is a real number there is no way to satisfy this equation.
Solving Quadratics by Grouping
Intro to grouping
Factor the following:
$$ \begin{align} 4x^{2} + 25x - 21 \end{align} $$First isolate $a$ and $b$ terms:
$$ \begin{align} a \cdot b = 4 \cdot -21 = -84\\ a + b = 25 \end{align} $$Now find for $a + b$:
$$ \begin{align} 1 + 84 \ne 25\\ 2 + 42 \ne 25\\ -3 + 28 = 25 \end{align} $$Now split $25x$ into two terms:
$$ \begin{align} 4x^{2} + 28x - 3x -21 \end{align} $$Note the placement of $-3x$ next to $-21$ since they have common factors, and the same for $4x^{2}$ and $28x$.
Now group the terms:
$$ \begin{align} (4x^{2} + 28x) + (-3x - 21) \end{align} $$Now, factor the groups:
$$ \begin{align} 4x(x + 7) + -3(x + 7) \end{align} $$And, finally, we can factor out $x + 7$ to get:
$$ \begin{align} (x + 7)(4x - 3) \end{align} $$Factoring by grouping
Example 3: Factoring: $3x^{2} - 6x - 4x + 8$
$$ \begin{align} 3x^{2} - 6x -4x + 8 \end{align} $$First, group terms:
$$ \begin{align} (3x^{2} - 6x) + (-4x + 8) \end{align} $$Then, factor out GCFs:
$$ \begin{align} 3x(x - 2) + (-4)(x - 2) \end{align} $$Factor out the common factor:
$$ \begin{align} (x - 2)(3x - 4) \end{align} $$[W]e factored out a $-4$ to reveal a common factor of $(x - 2)$ between the terms. If we instead factored out a positive $4$, we would not obtain that common binomial factor…
When the leading term in a group is negative, we will often need to factor out a negative common factor.
When can we use the grouping method?
The grouping method can be used to factor polynomials whenever a common factor exists between the groupings.
Factoring quadratics by grouping
Factor the following by grouping:
$$ \begin{align} 4y^{2} + 4y - 15 \end{align} $$First, find the product of $a$ and $c$:
$$ \begin{align} a \cdot c = 4 \cdot -15 = -60 \end{align} $$Next, we find values whose sum will be term $b$ ($4y$) and whose product will be $-60$:
$$ \begin{align} 5 + -12 \ne 4\\ -6 + 10 = 4 \end{align} $$Next, break up $4y$ into two terms; note the grouping of like terms:
$$ \begin{align} (4y^{2} - 6y) + (10y - 15) \end{align} $$Now, factor out the GCF for each:
$$ \begin{align} 2y(2y - 3) + 5(2y - 3) \end{align} $$Next, factor out $2y - 3$:
$$ \begin{align} (2y - 3)(2y + 5) \end{align} $$Factoring quadratics: common factor + grouping
Example
$$ \begin{align} 35k^{2} + 100k - 15 \end{align} $$First factor out $5$:
$$ \begin{align} 5(7k^{2} + 20k - 3) \end{align} $$Now, find two numbers whose sum is $20$ and whose product is $7 \cdot 3$:
$$ \begin{align} a \cdot c = 7 \cdot 3 = 21\\ a + b = 20 + (-1) = 20 \end{align} $$Now, we can group accordingly:
$$ \begin{align} 5(7k^{2} + 21k - k - 3) \end{align} $$And, factor:
$$ \begin{align} 5(7k(k + 3) -1(k + 3)) =\\ 5(7k - 1)(k + 3) \end{align} $$Factoring quadratics: negative common factor + grouping
Solve:
$$ \begin{align} -12f^{2} - 38f + 22 \end{align} $$Factor:
$$ \begin{align} -2(6f^{2} + 19f - 11) \end{align} $$Find $a \cdot c$:
$$ \begin{align} a \cdot c = -66 \end{align} $$Find two numbers that satisfy $a \cdot c = -66$ and $a + c = b$:
$$ \begin{align} -3 \cdot 22 = -66\\ -3 + 22 = 19 \end{align} $$Split the $f$-coefficient term, grouping terms with a common factor:
$$ \begin{align} -2((6f^{2} -3f) + (22f - 11)) \end{align} $$Factor:
$$ \begin{align} -2(3f(2f - 1) + (11(2f - 1))) \end{align} $$Undistribute $(2f - 1)$:
$$ \begin{align} -2(2f - 1)(3f + 11) \end{align} $$Factoring quadratics: Difference of squares
Difference of squares intro
A difference of squares is the difference between two quantities that have been squared.
Observe:
$$ \begin{align} x^{2} - 9 =\\ (x)^{2} - (3)^{2} =\\ (x + 3)(x - 3) \end{align} $$More generally:
$$ \begin{align} (x + a)(x - a) =\\ x^{2} + ax - ax - a^{2} =\\ x^{2} - a^{2} \end{align} $$Factoring quadratics: Difference of squares
Example 2: Factoring $4x^{2} - 9$
The leading coefficient does not have to [be] equal to 1 in order to use the difference of squares pattern.
$4x^{2}$ and $9$ are perfect squares, since $4x^{2} = (2x)^{2}$ and $9 = (3)^{2}$.
$$ \begin{align} 4x^{2} - 9 =\\ (2x)^{2} - (3)^{2} =\\ (2x + 3)(2x - 3) \end{align} $$Factoring difference of squares: leading coefficient $\ne 1$
Solve for:
$$ \begin{align} 45x^{2} - 125 \end{align} $$First, factor out the GCF:
$$ \begin{align} 5(9x^{2} - 25) \end{align} $$We can now factor to:
$$ \begin{align} 5(3x + 5)(3x - 5) \end{align} $$Factoring difference of squares: analyzing factorization
Factoring difference of squares: missing values
The polynomial expression
$$ \begin{align} 36y^{3} - 100y \end{align} $$can be factored as
$$ \begin{align} 4y(My + g)(My - g) \end{align} $$Let’s factor from the start:
$$ \begin{align} 36y^{3} - 100y =\\ 4y(9y^{2} - 25) =\\ 4y((3y)^{2} - 5^{2}) =\\ 4y(3y - 5)(3y + 5) \end{align} $$Factoring difference of squares: shared factors
What binomial factor do $m^{2} - 4m - 45$ and $6m^{2} - 150$ share?
Factor the first polynomial:
$$ \begin{align} m^{2} - 4m - 45 =\\ (m - 9)(m + 5) \end{align} $$Factor the second polynomial:
$$ \begin{align} 6m^{2} - 150 =\\ 6(m^{2} - 25) =\\ 6(m - 5)(m + 5) \end{align} $$The common factor is $(m + 5)$
How to factor a difference of squares with leading coefficient other than 1(example)
Given
$45x^{2} - 125$
we can solve knowing that
$a^2 - b^2 = (a + b)(a - b)$
First, we look at common factors that can be factored out
$5(9x^2 - 25)$
This problem now contains a difference of squares which can be factored out based on the formula above where a = 3x and b = 5.
$5(3x + 5)(3x - 5)$
Identifying perfect square trinomials
Consider that this perfect square trinomial
$(Ax + B)^2$
is the same as
$(Ax)^2 + ABx + ABx + B^2 = A^2x^2 + 2ABx + B2$
Given a triangle with the following sides, what is the perimeter?
$25x^2 + 20x + 4$
We can simplify by using the formula at the top since 25x² and 4 are perfect squares
$(5x)^2 + (2 \cdot 5 \cdot 2x) + 2^2 = (5x + 2)^2$
Similarly,
$25x^2 - 30x + 9 = (5x - 3)^2 \text{or } (-5x + 3)^2$
given the presence of negatives,
$a = 5, b = -3 \text{or } a = -5, b = 3$
How to factor a trinomial by taking a common factor then using “perfect square” form (example)
Given
$16x^3 + 24x^2 + 9x$
We can immediately recognize that x can be factored out to get
$x(16x^2 + 24x + 9)$
Now, we can recognize this as a perfect square trinomial since 16x^2 and 9 are perfect squares, and solve from there
$x((4x)^2 + (2 \cdot 4x \cdot 3) + 3^2) = x(4x + 3)^2$
How to factor a trinomial by taking a factor of (-1) and then using “perfect square” form (example)
Given
$-4t^2 - 12t - 9$
We can simplify first by removing the negative
$-1(4t^2 + 12t + 9)$
And now we can see the perfect square trinomial form
$-1((2t)^2 + (2t \cdot 3 \cdot 2) + 3^2) = -1(2t +3)^2$
How to find missing values in “perfect square” factorization (example)
The quadratic expression
$x^2 + 5x + c$
is a perfect square, and it can be factored as
$(x + d)^2$
Both c and d are positive rational numbers.
What does c equal, and what does d equal?
We first make the expression containing d similar to the expression containing c:
$(x + d)^2 = x^2 + 2dx + d^2$
Having established that
$x^2 + 5x + c = x^2 + 2dx + d^2$
we can determine that 5 = 2d, and c = d^2.
First, we can solve for d:
$d = 2/5$
now we can solve for c:
$c = \frac{2}{5}\cdot \frac{2}{5} = \frac{4}{25}$
Easily Solved
Some quadratic equations are solveable in their current form:
$$ \begin{align} x^{2} - 4x - 5 \end{align} $$$$ \begin{align} x = 5\\ \text{ or }\\ x = -1 \end{align} $$Solving by Completing the Square
Others that cannot be solved this way easily (using factoring), can be solved by “completing the square.”
$10x^{2} - 30x - 8 = 0$
First, factor out the leading coefficient:
$x^{2} - 3x - \frac{8}{10} = 0$
Reorganize that problem so that it can be solved by completing the square:
$x^{2} - 3x = \frac{4}{5}$
To find a square we divide the constant $3$ by $2$ and square it–this is added to both sides:
$x^{2} - 3x + \frac{9}{4} = \frac{4}{5} + \frac{9}{4} = 61/20$
We can now express a perfect square:
$(x - \frac{3}{2})^2 = \frac{61}{20}$
This can be simplified further
$x - \frac{3}{2} = \pm \sqrt{\frac{61}{20}}$
and finally we have
$x = \frac{3}{2} \pm \sqrt{\frac{61}{20}}$
Which is roughly $3.246$ or $-.246$
the Quadratic Formula
The quadratic formula is used to find the roots or zeros of quadratic equations.
Given a quadratic formula of the form
$ax^{2} + bx + c = 0$
we can find x with the quadratic formula
$x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$
Given
$x^{2} + 4x - 21 = 0$
We can plug in the following into the formula
$a = 1$, $b = 4$, and $c = -21$
to get
$x = \frac{-4 \pm \sqrt{4^{2} - 4(1)(-21)}}{2(1)}$
which is simplified to
$x = \frac{-4 \pm \sqrt{16 - 4(-21)}}{2}$
which is simplified to
$x = \frac{-4 \pm \sqrt{16 + 84}}{2}$
which is simplified to
$x = \frac{-4 \pm \sqrt{100}}{2}$
which is simplified to
$x = -2 \pm 5$
and
$x = -7, 3$
Understanding the quadratic formula
We can prove the quadratic formula from start to finish when we start out with
$ax^{2} + bx + c = 0$
by dividing all terms by $a$ first
$\frac{ax^{2}}{a} + \frac{b}{a}x + \frac{c}{a} = \frac{0}{a}$
we then subtract $c$ over $a$ from both sides
$x^{2} + \frac{b}{a}x = \frac{-c}{a}$
we can then complete the square
$x^{2} + \frac{b}{a}x + (\frac{b}{2a})^{2} = \frac{-c}{a} + (\frac{b}{2a})^{2}$
and simplify to
$(x + \frac{b}{2a})^{2} = \frac{b^{2}}{4a^{2}} + \frac{-c}{a}$
we can “convert” minus c over a so that we have
$(x + \frac{b}{2a})^{2} = \frac{b^{2}}{4a^{2}} - \frac{4ac}{4a^{2}}$
we can simplify the right side to
$(x + \frac{b}{2a})^{2} = \frac{b^{2} - 4ac}{4a^{2}}$
we can then take the square root of both sides to get
$x + \frac{b}{2a} = \frac{\sqrt{b^{2} - 4ac}}{2a}$
and finally
$x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$
How to determine the number of solutions of a quadratic equation
Given the quadratic equation
$x^{2} + 14x + 49 = 0$
we can determine the number of solutions for an equation by evaluating the discriminant which is
$b^{2} - 4ac$
if $b^{2} - 4ac > 0$ then two solutions exist
if $b^{2} - 4ac = 0$ then one solution exists
if $b^{2} - 4ac < 0$ then no real numbers are solutions
the last scenario results from the fact that you can’t take the square root of a negative number and get a real number
The quadratic formula
The quadratic formula (intro)
Given a quadratic equation:
$$ \begin{align} ax^{2} + bx + c = 0 \end{align} $$We can find $x$ using the quadratic formula:
$$ \begin{align} x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \end{align} $$Example:
$$ \begin{align} x^{2} + 4x - 21 = 0 \end{align} $$In this example $a = 1, b = 4, c = -21$:
$$ \begin{align} x = \frac{-4 \pm \sqrt{16 - 4 \cdot 1 \cdot 21}}{2}\\ x = \frac{-4 \pm \sqrt{100}}{2}\\ x = \frac{-4 \pm 10}{2}\\ x = -2 \pm 5\\ x = 3 \text{or} x = -7 \end{align} $$Understanding the quadratic formula
If you have a general quadratic equation like this:
$$ \begin{align} ax^{2} + bx + c = 0 \end{align} $$Then the formula will help you find the roots of a quadratic equation, i.e. the values of $x$ where this equation is solved.
The quadratic formula
$$ \begin{align} x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \end{align} $$Worked example
First we need to identify the values for $a$, $b$, and $c$ (the coefficients). First step, make sure the equation is in the format from above, $ax^{2} + bx + c = 0$:
$$ \begin{align} x^{2} + 4x - 21 = 0 \end{align} $$- $a$ is the coefficient in front of $x^{2}$, so here $a = 1$ (note that $a$ can’t equal $0$—the $x^{2}$ is what makes it a quadratic).
- $b$ is the coefficient in front of the $x$, so here $b = 4$.
- $x$ is the constant, or the term without any $x$ next to it, so here $c = -21$.
Then we plug $a$, $b$, and $c$ into the formula [and solve]:
$$ \begin{align} x = \frac{-4 \pm \sqrt{4^{2} - 4 \cdot 1 \cdot -21}}{2 \cdot 1}\\ x = \frac{-4 \pm \sqrt{16 - 4 \cdot -21}}{2}\\ x = \frac{-4 \pm \sqrt{16 + 84}}{2}\\ x = \frac{-4 \pm \sqrt{100}}{2}\\ x = \frac{-4 \pm 10}{2}\\ x = -2 \pm 5 \end{align} $$Therefore $x = 3$ or $x = -7$.
What does the solution tell us?
The two solutions are the $x$-intercepts of the equation, i.e. where the curve crosses the $x$-axis. The equation $x^{2} + 3x - 4 = 0$ looks like:
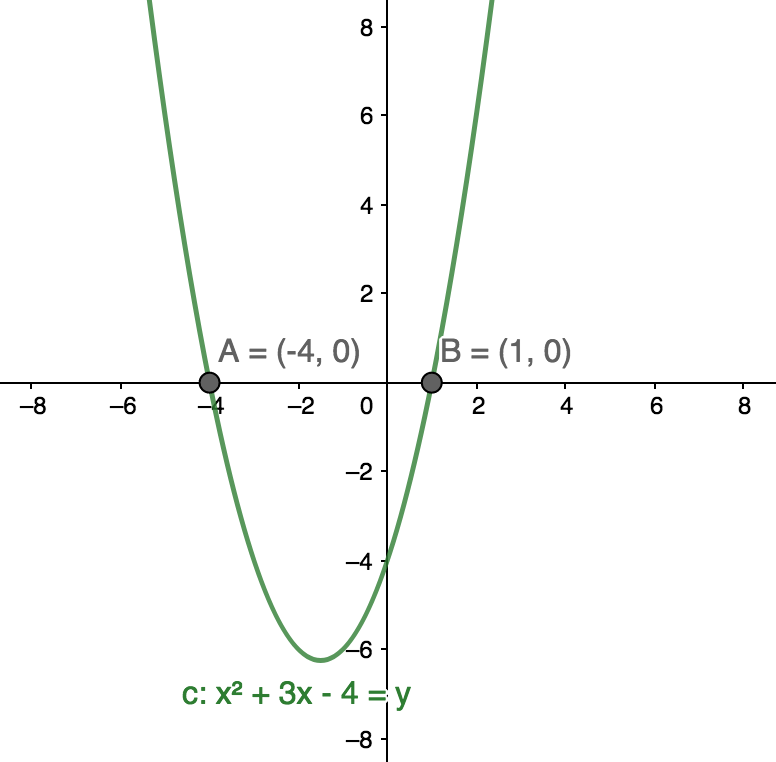
[W]hy do we need the [quadratic] formula?
Because sometimes quadratic equations are a lot harder to solve than that first example.
Second worked example
$$ \begin{align} 3x^{2} + 6x = -10 \end{align} $$[First, make sure] all terms are on the left-hand side:
$$ \begin{align} \underbrace{(3)}_{a}x^{2} + \underbrace{(6)}_{b}x + \underbrace{(10)}_{c} = 0 \end{align} $$The formula gives us:
$$ \begin{align} x = \frac{-6 \pm \sqrt{6^{2} - 4 \cdot 3 \cdot 10}}{2 \cdot 3}\\ x = \frac{-6 \pm \sqrt{36 - 120}}{6}\\ x = \frac{-6 \pm \sqrt{-84}}{6} \end{align} $$[Y]ou can’t take the square root of a negative number without using imaginary numbers, so that tells us there’s no real solutions to this equation. This means at no point will $y = 0$, the function won’t intercept the $x$-axis. We can also see this when graphed on a calculator:
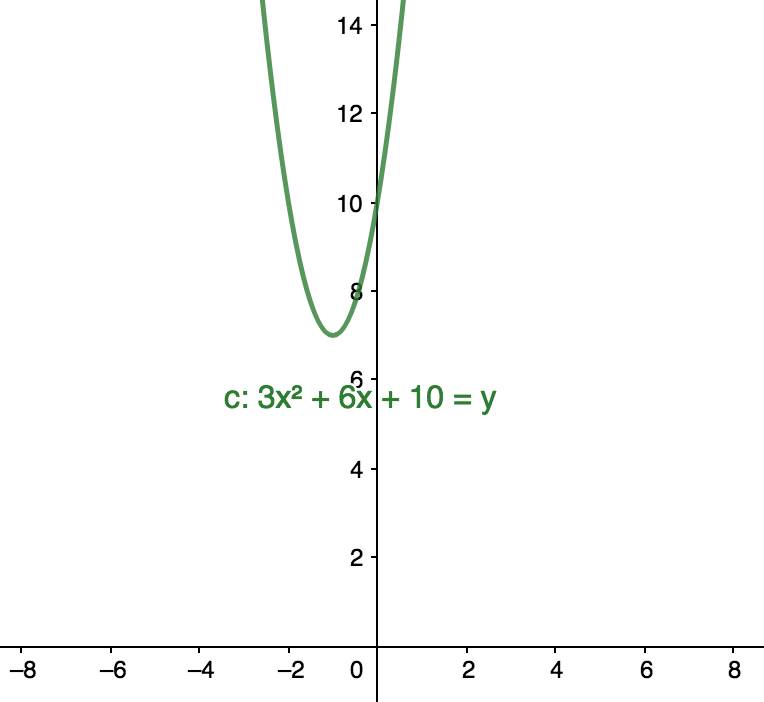
Tips when using the quadratic formula
- Be careful that the equation is arranged in the right form: $ax^{2} + bx + c = 0$ or it won’t work!
- Make sure you take the square root of the whole $(b^{2} - 4ac)$, and that $2a$ is the denominator of everything above it
- Watch your negatives: $b^{2}$ can’t be negative, so if $b$ starts as negative, make sure it changes to a positive since the square of a negative or a positive is a positive
- Keep the $\pm$ and always be on the look out for TWO solutions
- If you use a calculator, the answer might be rounded to a certain number of decimal places. If asked for the exact answer (as usually happens) and the square roots can’t be easily simplified, keep the square roots in the answer, e.g. $\frac{2 - \sqrt{10}}{2}$ and $\frac{2 + \sqrt{10}}{2}$
Using the quadratic formula
Solve
$$ \begin{align} 0 = -7q^{2} + 2q + 9 \end{align} $$Plug-in values:
$$ \begin{align} x = \frac{-2 \pm \sqrt{2^{2} - 4(-7)(9)}}{2(-7)}\\ x = \frac{-2 \pm \sqrt{4 + 252}}{-14}\\ x = \frac{-2 \pm \sqrt{256}}{-14}\\ x = \frac{-2 \pm 16}{-14}\\ x = \frac{-1 \pm 8}{-7} \end{align} $$$x = -1$ or $x = \frac{9}{7}$
We can verify that $-1$ is a solution by plugging it into the original equation:
$$ \begin{align} 0 = -7(-1)^{2} + 2(-1) + 9\\ 0 = -7(1) + -2 + 9\\ 0 = -9 + 9\\ 0 = 0 \end{align} $$Worked example quadratic formula
Rewrite the equation $6x^{2} + 3 = 2x - 6$ in standard form and identify $a$, $b$, and $c$.
$$ \begin{align} 6x^{2} + 3 = 2x - 6\\ 6x^{2} + 3 + 6 - 2x = 0\\ \underbrace{6}_{a}x^{2} - \underbrace{2}_{b}x + \underbrace{9}_{c} = 0 \end{align} $$Worked example: quadratic formula (example 2)
Solve:
$$ \begin{align} -x^{2} + 8x = 1 \end{align} $$First, setup the question in standard form:
$$ \begin{align} -x^{2} + 8x = 1\\ x^{2} - 8x + 1 = 0 \end{align} $$Next, solve using the quadratic equation:
$$ \begin{align} x = \frac{-(-8) \pm \sqrt{-8^{2} - 4(1)(1)}}{2(1)}\\ x = \frac{8 \pm \sqrt{64 - 4}}{2}\\ x = \frac{8 \pm \sqrt{60}}{2}\\ x = \frac{8 \pm 2\sqrt{15}}{2}\\ x = 4 \pm \sqrt{15} \end{align} $$The solutions are $x = 4 - \sqrt{15}$ or $x = 4 + \sqrt{15}$
Worked example: quadratic formula (negative coefficients)
Solve
$$ \begin{align} -3x^{2} + 10x - 3 = 0 \end{align} $$Plug in values for the quadratic equation:
$$ \begin{align} x = \frac{-10 \pm \sqrt{10^{2} - 4 \cdot -3 \cdot -3}} {2 \cdot -3}\\ = \frac{-10 \pm \sqrt{100 - 36}} {-6}\\ = \frac{-10 \pm \sqrt{64}} {-6}\\ = \frac{-10 \pm 8} {-6}\\ = \frac{-5 \pm 4} {-3}\\ \end{align} $$$x = \frac{1}{3}$ or $x = 3$
You also could’ve rearranged $-3x^{2} + 10x - 3 = 0$ to $3x -10x + 3 = 0$.
Using the quadratic formula: number of solutions
Determine the number of solutions to the quadratic equation
$$ \begin{align} x^{2} + 14x + 49 = 0 \end{align} $$Given the quadratic formula:
$$ \begin{align} x = \frac{-b \pm \sqrt{b^{2} - 4ac}}\\ {2a} \end{align} $$- If $b^{2} - 4ac > 0$ then there are 2 solutions for $x$.
- If $b^{2} - 4ac = 0$ then there is 1 solution.
- If $b^{2} - 4ac < 0$ then there are no solutions as you cannot obtain a real number from a negative square root.
$b^{2} - 4ac$ determines the number of solutions; it is known as the discriminant.
$$ \begin{align} 14^{2} - 4 \cdot 1 \cdot 49 =\\ 196 - 196 = 0 \end{align} $$There is 1 solution for $x^{2} + 14x + 49 = 0$.
Let’s prove this:
$$ \begin{align} \frac{-14 \pm \sqrt{14^{2} - 4 \cdot 1 \cdot 49}} {2 \cdot 1} =\\ \frac{-14 \pm \sqrt{0}} {2} = \\ \frac{-14} {2} =\\ -7 \end{align} $$The solution is $x - 7$.
Proof of the quadratic formula
We know that given an equation in standard form:
$$ \begin{align} ax^{2} + bx + c = 0 \end{align} $$We can solve for $x$ with the quadratic formula
$$ \begin{align} x = \frac{-b \pm \sqrt{b^{2} - 4ac}}\\ {2a} \end{align} $$Here is how we get to the quadratic formula from standard form:
$$ \begin{align} ax^{2} + bx + c = 0\\ x^{2} + \frac{b}{a}x + \frac{c}{a} = \frac{0}{a} \\ x^{2} + \frac{b}{a}x = - \frac{c}{a} \\ \end{align} $$At this point we complete the square:
$$ \begin{align} x^{2} + \frac{b}{a}k + (\frac{b}{2a})^{2} = - \frac{c}{a} + (\frac{b}{2a}) \end{align} $$Thus, giving us:
$$ \begin{align} (x + \frac{b}{2a})^{2} = -\frac{c}{a} + (\frac{b}{2a})^{2}\\ \end{align} $$We know this because:
$$ \begin{align} (x + \frac{b}{2a})(x + \frac{b}{2a}) \\ x^{2} + \frac{b}{2a}x + \frac{b}{2a}x + (\frac{b}{2a})^{2}\\ x^{2} + \frac{b}{a}x + (\frac{b}{2a})^{2} \end{align} $$Continuing
$$ \begin{align} (x + \frac{b}{2a})^{2} = -\frac{c}{a} + (\frac{b}{2a})^{2}\\ (x + \frac{b}{2a})^{2} = -\frac{c}{a} + \frac{b^{2}}{4a^{2}}\\ (x + \frac{b}{2a})^{2} = -\frac{4ac}{4a^{2}} + \frac{b^{2}}{4a^{2}}\\ (x + \frac{b}{2a})^{2} = \frac{b^{2} -4ac}{4a^{2}}\\ x + \frac{b}{2a} = \sqrt{\frac{b^{2} -4ac}{4a^{2}}}\\ x + \frac{b}{2a} = \frac{\sqrt{b^{2} -4ac}}{\sqrt{4a^{2}}}\\ x + \frac{b}{2a} = \frac{\sqrt{b^{2} -4ac}}{2a}\\ x = \frac{-b \pm \sqrt{b^{2} -4ac}}{2a} \end{align} $$Solving quadratics with the quadratic formula
Given a quadratic equation in standard form:
$$ \begin{align} ax^{2} + bx + c = 0 \end{align} $$We can find $x$ using the quadratic formula:
$$ \begin{align} x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \end{align} $$Example:
$$ \begin{align} x^{2} + 4x - 21 = 0 \end{align} $$In this example $a = 1, b = 4, c = -21$:
$$ \begin{align} x = \frac{-4 \pm \sqrt{16 - 4 \cdot 1 \cdot 21}}{2}\\ x = \frac{-4 \pm \sqrt{100}}{2}\\ x = \frac{-4 \pm 10}{2}\\ x = -2 \pm 5\\ x = 3 \text{or} x = -7 \end{align} $$Proof of the quadratic formula
We know that given an equation in standard form:
$$ \begin{align} ax^{2} + bx + c = 0 \end{align} $$We can solve for $x$ with the quadratic formula
$$ \begin{align} x = \frac{-b \pm \sqrt{b^{2} - 4ac}}\\ {2a} \end{align} $$Here is how we get to the quadratic formula from standard form:
$$ \begin{align} ax^{2} + bx + c = 0\\ x^{2} + \frac{b}{a}x + \frac{c}{a} = \frac{0}{a} \\ x^{2} + \frac{b}{a}x = - \frac{c}{a} \\ \end{align} $$At this point we complete the square:
$$ \begin{align} x^{2} + \frac{b}{a}k + (\frac{b}{2a})^{2} = - \frac{c}{a} + (\frac{b}{2a}) \end{align} $$Thus, giving us:
$$ \begin{align} (x + \frac{b}{2a})^{2} = -\frac{c}{a} + (\frac{b}{2a})^{2}\\ \end{align} $$We know this because:
$$ \begin{align} (x + \frac{b}{2a})(x + \frac{b}{2a}) \\ x^{2} + \frac{b}{2a}x + \frac{b}{2a}x + (\frac{b}{2a})^{2}\\ x^{2} + \frac{b}{a}x + (\frac{b}{2a})^{2} \end{align} $$Continuing
$$ \begin{align} (x + \frac{b}{2a})^{2} = -\frac{c}{a} + (\frac{b}{2a})^{2}\\ (x + \frac{b}{2a})^{2} = -\frac{c}{a} + \frac{b^{2}}{4a^{2}}\\ (x + \frac{b}{2a})^{2} = -\frac{4ac}{4a^{2}} + \frac{b^{2}}{4a^{2}}\\ (x + \frac{b}{2a})^{2} = \frac{b^{2} -4ac}{4a^{2}}\\ x + \frac{b}{2a} = \sqrt{\frac{b^{2} -4ac}{4a^{2}}}\\ x + \frac{b}{2a} = \frac{\sqrt{b^{2} -4ac}}{\sqrt{4a^{2}}}\\ x + \frac{b}{2a} = \frac{\sqrt{b^{2} -4ac}}{2a}\\ x = \frac{-b \pm \sqrt{b^{2} -4ac}}{2a} \end{align} $$Quadratic Equations
Standard Form
$$ \begin{align} f(x) = ax^{2} + bx + c \end{align} $$Completing the Square
- use to convert to vertex form
When $a$ term is not 1
Given
$$ \begin{align} 12x^2 + 11x + 2 \end{align} $$Multiply the $a$ coefficient by $c$.
$$ \begin{align} 12 \cdot 2 = 24 \end{align} $$The $b$ coefficient may be a combination of factors of $\pm a \cdot c$. In this case $12$ and $2$ are the factors we need to create the middle term to arrive at:
Quadratic Formula
- used to find the value(s) of $x$ where $y = 0$ in a quadratic formula written in standard form
Finding the Vertex
Use $f(h) = k$, with the vertex at $(h, k)$.
$$ \begin{align} h = \frac{-b}{2a} \end{align} $$Vertex / Graphing Form
- in this form the vertex is $(-h, k)$
Substitution of $x^2$
- $u$ for $x^2$ for formulas of the $ax^4 + bx^2 + c$
Factoring Quadratics Intro
Given the quadratic expression:
$$ \begin{align} x^{2} - 3x - 10 \end{align} $$We’re going to re-write the expression as the product of two binomials:
$$ \begin{align} (x + a)(x + b) \end{align} $$First, re-write the original expression with $a$ and $b$:
$$ \begin{align} x^{2} + ax + bx + ab =\\ x^2 + (a + b)x + ab \end{align} $$From this we can infer that:
$$ \begin{align} a + b = -3\\ a \cdot b = -10\\ \end{align} $$We can factor $10$ such that the sum of the two terms is $-3$:
$$ \begin{align} 2 \cdot -5\\ a = 2\\ b = -5 \end{align} $$We can now re-write the original equation as:
$$ \begin{align} (x + 2)(x - 5) \end{align} $$Factoring quadratics: leading coefficient = 1
Factoring a polynomial involves writing it as a product of two or more polynomials. It reverses the process of polynomial multiplication.
Let’s consider the expression:
$$ \begin{align} (x + 2)(x + 4) \end{align} $$We can find the product by applying the distributive property multiple times.
$$ \begin{align} (x + 2)(x + 4) = (x + 2)(x) + (x + 2)(4)\\ = x^{2} + 2x + 4x + 8\\ = x^{2} + 6x + 8 \end{align} $$From this, we see that $x + 2$ and $x + 4$ are factors of $x^{2} + 6x + 8$, but how would we find these factors if we didn’t start with them?
We can reverse the process of binomial multiplication shown above in order to factor a trinomial (which is a polynomial with three terms.
To factor $x^{2} + 5x + 6$, we first need to find two numbers that multiply to $6$ (the constant number) and add up to $5$ (the $x$-coefficient).
These two numbers are $-2$ and $-3$[:]
$$ \begin{align} x^{2} - 5x + 6 = (x - 2)(x - 3) \end{align} $$The sum-product pattern
Let’s repeat what we just did with $(x + 2)(x + 3)$ for $(x + m)(x + n)$:
$$ \begin{align} (x + m)(x + n) = (x + m)(x) + (x + m)(n) =\\ x^{2} + mx + nx + m \cdot n =\\ x^{2} + (m + n)x + m \cdot n \end{align} $$This is called the sum-product pattern.
In general, [this] is only applicable when we can actually write a trinomial as $(x + m)(x + n)$ for some integers $m$ and $n$.
This means that the leading term of the trinomial must be $x^{2}$ (and not, for instance, $2x^{2}$) in order to even consider this method.
However, not all trinomials with $x^{2}$ as a leading term can be factored e.g. $x^{2} + 2x + 2$ cannot be factored because there are no two integers whose sum is $2$ and whose product is $2$.
Factoring quadratics as $(x + a)(x + b)$ (example 2)
[Factor the following to the form $(x + a)(x +b)$:
$$ \begin{align} x^{2} - 14x + 40 =\\ a + b = -14 \\ a \cdot b = 40 \end{align} $$We can determine that determine the following:
$$ \begin{align} a = -4\\ b = -10 \end{align} $$And, finally:
$$ \begin{align} (x - 4)(x - 10) \end{align}
$$
More examples of factoring quadratics as $(x + a)(x + b)$
Factoring quadratics: leading coefficient $\ne 1$
Why is this method working?
Suppose the general quadratic expression $ax^{2} + bx + c$ can be factored as
$$ \begin{align} (Ax + B)(Cx + D) \end{align} $$with integers A, B, C, and D.
When we expand the parentheses, we obtain the quadratic expression
$$ \begin{align} (AC)x^{2} + (BC + AD)x + BD \end{align} $$Since this expression is equivalent to $ax^{2} + bx + c$, the corresponding coefficients in the two expressions must be equal! This gives us the following relationship between all unknown letters:
$$ \begin{align} a = AC\\ b = (BC + AD)\\ c = BD \end{align} $$Now, let’s define $m = BC$ and $n = AD$.
According to this definition:
$$ \begin{align} m + n = BC + AD = b\\ m \cdot n = (BC)(AD) = (AC)(BD) = a \cdot c \end{align} $$And so $BC$ and $AD$ are the two integers we are always looking for when we use this factorization method!
The next step in the method after finding $m$ and $n$ is to split the $x$-coefficient ($b$) according to $m$ and $n$ and factor using grouping.
Indeed, if we split the $x$-term $(BC + AD)x$ in $(BC)x + (AD)x$, we will be able to use grouping to factor our expression back into $(Ax + B)(Cx + D)$.
$$ \begin{align} (AC)x^{2} + (BC + AD)x + BD =\\ ACx^{2} + BCx + ADx + BD =\\ (ACx^{2} + BCx) + (ADx + BD) =\\ Cx(Ax + B) + D(Ax + B) =\\ (Cx + D)(Ax + B) \end{align} $$Factoring polynomials with quadratic forms
Factoring two-variable quadratics
A simple example:
$$ \begin{align} x^{2} + 4x - 5 =\\ (x - 1)(x + 5) \end{align} $$Factor the following
$$ \begin{align} x^{2} + 4xy - 5y^{2} \end{align} $$We can rewrite it such that $4y$ is a coefficient on the $x$ term:
$$ \begin{align} x^{2} + 4y(x) - 5y^{2} \end{align} $$Finally, we can factor to:
$$ \begin{align} (x - y)(x + 5y) \end{align} $$Factoring two-variable quadratics: rearranging
Factor the following:
$$ \begin{align} 30x^{2} + 11xy + y^{2} \end{align} $$First, rearrange the problem so that the term with the coefficient of $1$ is at the beginning:
$$ \begin{align} y^{2} + 11xy + 30x^{2} \end{align} $$Now, find two numbers whose product is $30$ and whose sum is $11$ to solve:
$$ \begin{align} (y + 5x)(y + 6x) \end{align} $$Factoring two-variable quadratics: grouping
Solve the following:
$$ \begin{align} 5rs + 25r - 3s - 15 \end{align} $$First group the terms appropriately:
$$ \begin{align} (5rs + 25r) + (-3s - 15) \end{align} $$Then factor out GCFs:
$$ \begin{align} 5r(s + 5) + -3(s + 15) \end{align} $$And, now, factor out $(s + 15)$:
$$ \begin{align} (s + 5)(5r - 3) \end{align} $$Perfect square factorization intro
Example:
$$ \begin{align} x^{2} + 6x + 9 =\\ (x + 3)(x + 3) \end{align} $$Example:
$$ \begin{align} a^{2} + 14a + 49 =\\ (a + 7)(a + 7) \end{align} $$Factoring quadratics: Perfect squares
Intro: Factoring perfect square trinomials
To expand any binomial, we can apply one of the following patterns.
- $(a + b)^{2} = a^{2} + 2ab + b^{2}$
- $(a - b)^{2} = a^{2} - 2ab + b^{2}$
The reverse of this expansion process is a form of factoring.
- $a^{2} + 2ab + b^{2} = (a + b)^{2}$
- $a^{2} - 2ab + b^{2} = (a - b)^{2}$
We can apply the first pattern to factor $x^{2} + 10x + 25$:
$$ \begin{align} x^{2} + 10x + 25 =\\ x^{2} + 2(x)(5) + (5)^{2} =\\ (x + 5)^{2} \end{align} $$Expressions of this form are called perfect square trinomials. The name reflects the fact that this type of three termed polynomial can be expressed as a perfect square!
Example 2: Factoring $4x^{2} + 12x + 9$
It is not necessary for the leading coefficient of a perfect square trinomial to be $1$.
For example, in $4x^{2} + 12x + 9$, notice that both the first and last terms are perfect squares: $4x^{2} = (2x)^{2}$ and $9 = (3)^{2}$. Additionally, notice that the middle term is two times the product of the numbers that are squared: $2(2x)(3) = 12$.
Because it satisfies the above conditions, $4x^{2} + 12x + 9$ is also a perfect square trinomial. We can again apply the following factoring pattern.
$$ \begin{align} a^{2} + 2ab + b^{2} = (a + b)^{2} \end{align} $$In this case, $a = 2x$ and $b = 3$. The polynomial factors as follows:
$$ \begin{align} 4x^{2} + 12x + 9 = (2x)^{2} + 2(2x)(3) + (3)^{2}\\ = (2x + 3)^{2} \end{align} $$Factoring perfect squares
Factor:
$$ \begin{align} 25x^{2} - 30x + 9 \end{align} $$Notice $25x^{2}$ and $9$ are perfect squares…
Can we model this problem as perfect square binomial of the form $(a + b)^{2}$?
$$ \begin{align} (ax + b)^{2} =\\ (ax + b)(ax + b) =\\ a^{2}x^{2} + abx + abx + b^{2} a^{2}x^{2} + 2abx + b^{2} \end{align} $$Substitute in the appropriate terms:
$$ \begin{align} 25x^{2} - 30x + 9 \end{align} $$Note that $a^{2}$ is $25$ and $b^{2}$ is $9$, both are perfect squares.
Given that $2ab$ is negative, $a = \pm 5$ or $b = \pm 3$.
The factored trinomial is satisfied by:
$$ \begin{align} (5x - 3)^{2} \end{align} $$And
$$ \begin{align} (3 - 5x)^{2} \end{align} $$Identifying perfect square form
By working from the factored form we can find the pattern for trinomials that are perfect squares:
$$ \begin{align} (Ax + B)^{2} =\\ (Ax + B)(Ax + B) = \\ (Ax)^{2} + ABx + ABx + B^{2} =\\ (Ax)^{2} + 2ABx + B^{2} =\\ A^{2}x^{2} + 2ABx + B^{2} \end{align} $$The following perfect square matches this pattern. We can verify this by working back to the squared binomial form using the pattern above:
$$ \begin{align} 25x^{2} + 20x + 4 =\\ (5)^{2}x^{2} + 2(5)(2) + (2)^{2} =\\ (5x + 2)^{2} \end{align} $$Factoring perfect squares: common factor
Given
$$ \begin{align} 16x^{3} + 24x^{2} + 9x \end{align} $$First, we can find a common factor:
$$ \begin{align} x(16x^{2} + 24x + 9) \end{align} $$Then, we can continue accordingly:
$$ \begin{align} x((4x)^{2} + 2(4x)(3) + 3^{2}) x(4x + 3)^{2} \end{align} $$Factoring perfect squares: negative common factor
Given
$$ \begin{align} -4t^{2} - 12t - 9 \end{align} $$We can factor out $-1$ as a common factor:
$$ \begin{align} -1(4t^{2} + 12t + 9) \end{align} $$And, now we can factor it to a perfect square binomial:
$$ \begin{align} -1((2t)^{2} + (2)(2)(3) + (3)^{2}) =\\ -1(2t + 3) \end{align} $$Factoring perfect squares: missing values
The quadratic expression $x^{2} + 5x + c$ is a perfect square, and it can be factored as $(x + d)^{2}$. Both $c$ and $d$ are positive rational numbers. What are they equal to?
We can establish the following:
$$ \begin{align} x^{2} + 5x + c =\\ (x + d)^{2} =\\ x^{2} + 2dx + d^{2} \end{align} $$We can establish the following:
$$ \begin{align} 2d = 5\\ d = \frac{5}{2}\\ c =\\ d^{2} =\\ (\frac{5}{2})^{2} =\\ \frac{25}{4} \end{align} $$Factoring perfect squares: shared factors
The quadratic expressions $4x^{2} + 12x + 9$ and $4x^{2} - 9$ share a common binomial factor. What binomial factor do they share?
Factor each and see if they share a common binomial factor…
$$ \begin{align} 4x^{2} + 12x + 9 =\\ (2)^{2}x^{2} + 2(2)(3) + (3)^{2} =\\ (2x + 3)^{2} \end{align} $$$$ \begin{align} 4x^{2} - 9 =\\ (2)^{2}x^{2} - (2)(3) + (2)(3) + (3)(-3) =\\ (2x - 3)(2x + 3) \end{align} $$They both share $(2x + 3)$…
Strategy in factoring quadratics
Strategy in factoring quadratics (part 1 of 2)
Strategy in factoring quadratics (part 2 of 2)
Factoring quadratics in any form
Factoring polynomials with special product forms
Factoring perfect squares: 4th degree polynomial
Factor:
$$ \begin{align} 25x^{4} - 30x^{2} + 9 \end{align} $$Note that all terms are perfect squares.
We can re-express the problem as:
$$ \begin{align} (\pm 5x^{2})^{2} - 30x^{2} + (\pm 3)^{2} \end{align} $$And solve:
$$ \begin{align} (5x^{2} - 3)^{2} \end{align} $$Factoring difference of squares: two variables
Factor:
$$ \begin{align} x^{2} - 49y^{2} \end{align} $$Recall the pattern $(a + b)(a - b) = a^{2} - b^{2}$, and rewrite:
$$ \begin{align} (x^{2} - 7y)(x^{2} + 7y) \end{align} $$Factoring difference of squares: two variables (example 2)
Factor:
$$ \begin{align} 49x^{2} - 49y^{2} \end{align} $$Recall the pattern $(a + b)(a - b) = a^{2} - b^{2}$, and rewrite:
$$ \begin{align} (7x^{2} - 7y^{2})(7x^{2} + 7y^{2}) \end{align} $$Then factor out the $7$:
$$ \begin{align} 7(x + y)7(x - y) =\\ 49(x + y)(x - y) \end{align} $$You may also factor out the $49$ at the start…
#Introduction to Polynomial Factorization
actoring polynomials with special product forms
Introduction to polynomials
The name polynomial means many names. A polynomial is the sum of a finite number of terms where each term is a coefficient multiplied by a variable raised to a non-negative integer power.
$$ \begin{align} Ax^n \end{align} $$A coefficient is a number that is in front of the variable. The variable is multiplied by a coefficient.
Examples include:
$$ \begin{align} 10x^7 - 9x^2 + 15x^3 + 9\\ 9a^2 - 5\\ 6\\ 7y^2 - 3y + \pi \end{align} $$The following are not polynomials:
$$ \begin{align} 10x^{-7} - 9x\\ 9a^{\frac{1}{2}} - 5 \end{align} $$A monomial is polynomial with a single term. A binomial is a polynomial with two terms. A trinomial is a polynomial with three terms.
The degree of a term is the exponent of the term.. The degree of a polynomial is the exponent of the term with the largest exponent.
A polynomial in standard form is polynomial written with degrees in descending order. The leading term is the term with the highest degree. The leading coefficient is the coefficient on the leading term.
Simplify:
$$ \begin{align} (5x^2 + 8x - 3) + (2x^2 - 7x + 13x) \end{align} $$Remove the parentheses
$$ \begin{align} 5x^2 + 8x - 3 + 2x^2 - 7x + 13x \end{align} $$Add like terms:
$$ \begin{align} 7x^2 + 14x - 3 \end{align} $$This cannot be simplified further.
#Old content – content that belongs in missions other than Algebra 1. This content will be removed from Algebra 1 soon.
Quadratic factored form
Graphing quadratics in factored form
Graph:
$$ \begin{align} y = \frac{1}{2}(x - 6)(x + 2) \end{align} $$The key insight is that you’ll get a quadratic by multiplying this out, and that it is a parabola.
First, we’ll solve where $x = 0$ as this tells us where the parabola intersects the $x$-axis:
$$ \begin{align} \frac{1}{2}(x - 6)(x + 2) = 0 \end{align} $$$x$ is $0$ when $x - 6 = 0$ or $x + 2 = 0$
We determine that:
$$ \begin{align} x = 6 \end{align} $$$$ \begin{align} x = -2 \end{align} $$Since the vertex lies between these two values for $x$, we can determine the $x$ value for the vertex to be:
$$ \begin{align} 6 + (-2) / 2 = 2 \end{align} $$Plugging this value into our original equation as $x$ gives us the $y$ value for the vertex:
$$ \begin{align} y = \frac{1}{2}(2 - 6)(2 + 2) =\\ \frac{1}{2}(-4)(4) =\\ \frac{1}{2}(-16) =\\ -8 \end{align} $$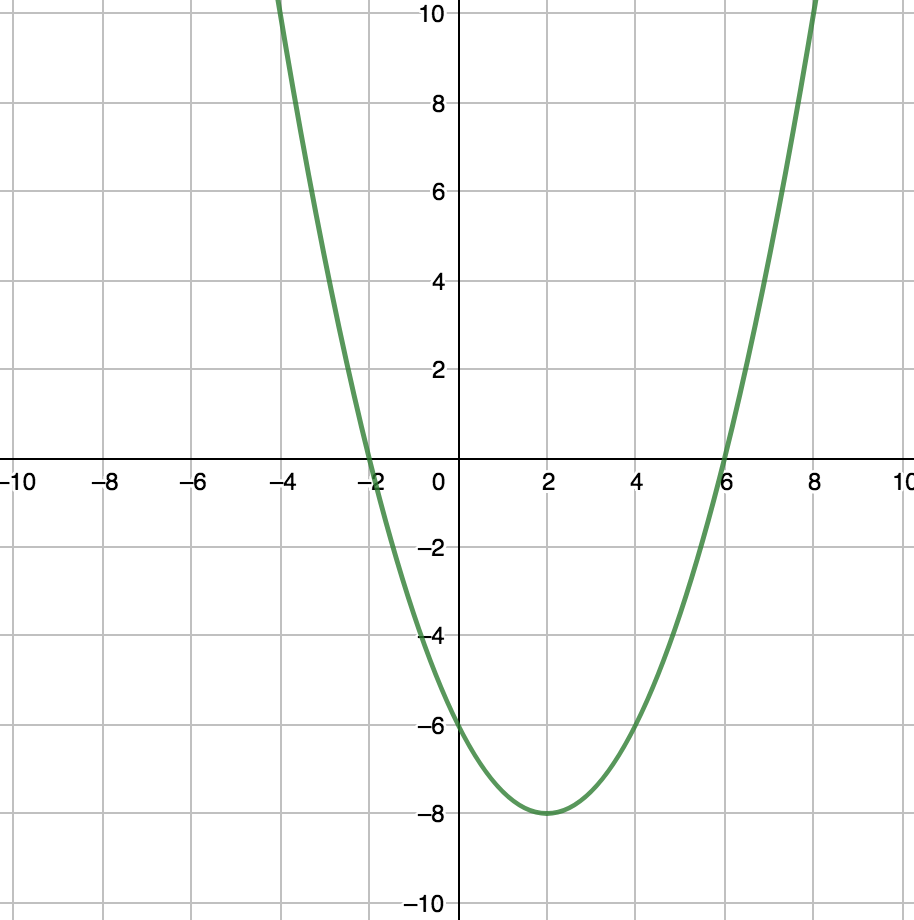
Quadratic word problems (factored form)
A rocket is launched from a platform. Its height (in meters), $x$ seconds after the launch, is modeled by
$$ \begin{align} h(x) = -4(x + 2)(x - 18) \end{align} $$What is the height of the rocket at the time of launch?
The time of launch is $0$ seconds. We can plug that in right away to obtain the $y$-value (height):
$$ \begin{align} -4(0 + 2)(0 - 18) =\\ 144 \end{align} $$How many seconds after launch will the rocket hit the ground?
Let’s find the two $x$-intercepts—the higher of the two will represent the time when the rocket hits the ground (0 meters):
$$ \begin{align} x + 2 = 0\\ x = -2 \end{align} $$And
$$ \begin{align} x - 18 = 0\\ x = 18 \end{align} $$How many seconds after being launched will the rocket reach its maximum height?
The parabola will have the highest $y$-value exactly between the $x$-intercepts (the axis of symmetry):
$$ \begin{align} (-2 + 18)/ 2 =\\ 16/2 = 8 \end{align} $$What is the maximum height that the rocket will reach?
We can find this with the $x$-value for the axis of symmetry:
$$ \begin{align} -4(8 + 2)(8 - 18) =\\ -4(10)(-10) =\\ 400 \end{align} $$Solving quadratics by taking square roots
Solving quadratics by taking square roots (example)
Solve for $x$:
$$ \begin{align} 2x^{2} + 3 = 75\\ 2x^{2} = 72\\ x^{2} = 36\\ x = \pm 6 \end{align} $$Solving quadratics by taking square roots (lesson summary)
So far you have solved linear equations, which include constant terms—plain numbers—and terms with the variable raised to the first power, $x^{1} = x$.
You will now learn how to solve quadratic equations, which include terms where the varaible is raised to the second power, $x^{2}$.
Here are a few examples[:]
$$ \begin{align} x^{2} = 36\\ (x - 2)^{2} = 49\\ 2x^{2} + 3 = 131 \end{align} $$Solving $x^{2} = 36$ and similar equations
$$ \begin{align} x^{2} = 36 \sqrt{x} = \sqrt{36} x \pm 6 \end{align} $$Note that every positive number has two square roots…
When we solved linear equations, we isolated the variable by using inverse operations: If the variable had $3$ added to it, we subtracted $3$ from both sides [etc.]
The inverse operation of taking the square is taking the square root. However… we must remember to take both the positive and the negative square roots.
Solving $(x - 2)^{2} - 49$ and similar equations
$$ \begin{align} (x - 2)^{2} = 49\\ \sqrt{(x - 2)^{2}} \pm \sqrt{49}\\ x - 2 = \pm 7 x = \pm 7 + 2 \end{align} $$Therefore, the solutions are $x = 9$ and $x = -5$
Suppose we wanted to expand the parentheses[:]
$$ \begin{align} x^{2} - 4x + 4 = 49 \end{align} $$If we wanted to take the square root in this equation, we would have to take the square root of $x$. But this gives us $\sqrt{x}$, which is not helpful.
Solving $2x^{2} + 3 = 131$ and similar equations
Not all quadratic equations are solved immediately taking the square root. Sometimes we have to isolate the squared term before taking its root.
$$ \begin{align} 2x^{2} + 3 = 131\\ 2x^{2} = 128\\ x^{2} = 64\\ \sqrt{x^{2}} = \pm \sqrt{64}\\ x = \pm 8 \end{align} $$Solving quadratics by taking square roots examples
$$ \begin{align} (x + 3)^{2} - 4 = 0\\ (x + 3)^{2} = 4\\ x + 3 = \pm 2\\ x = -1 \text{and} x = -5 \end{align} $$Given the following, at what $x$ values does the graph intersect the $x$-axis?
$$ \begin{align} f(x) = (x - 2)^{2} - 9 \end{align} $$Basically, we want to find solutions such that $f(x) = 0$:
$$ \begin{align} (x - 2)^{2} - 9 = 0 \\ (x - 2)^{2} = 9 \\ x - 2 = \pm 3 \\ x = 5 \text{and} x = -1 \end{align} $$Solving quadratics by taking square roots: strategy
Quadratics by taking square roots: with steps
Solving simple quadratics
Vertex form introduction
The same quadratic equation can be expressed three different ways:
Standard form
$$ \begin{align} y = 3x^{2} + 12x - 15 \end{align} $$Quadratic in factored form
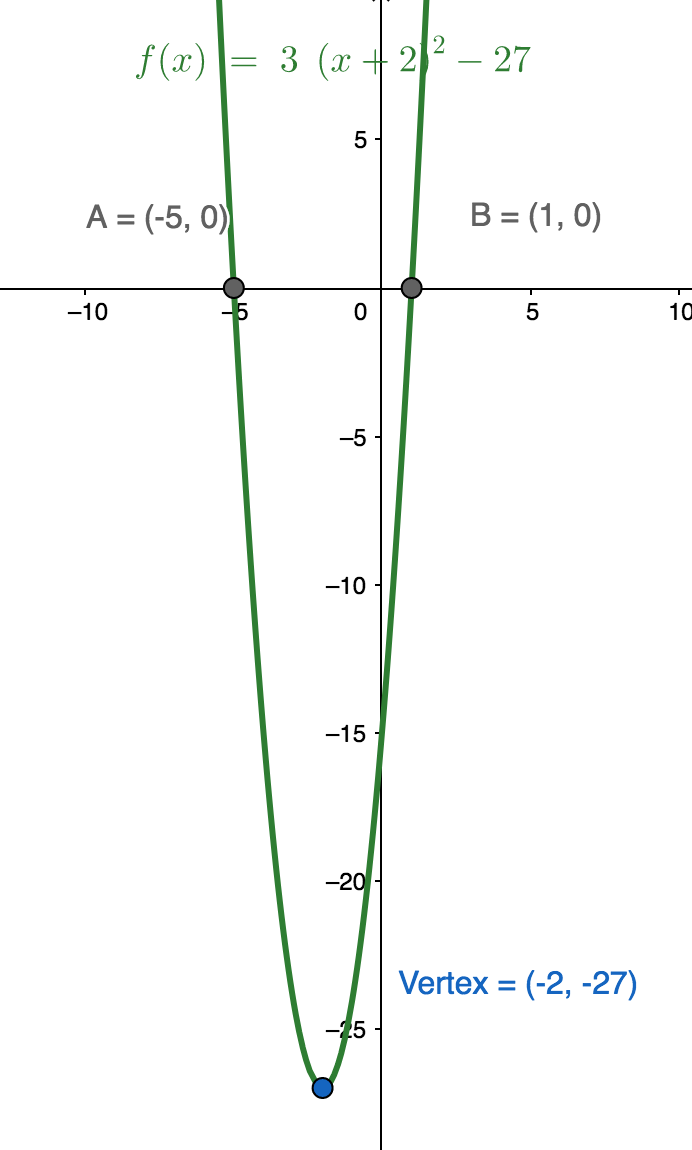
$$ \begin{align} y = 3(x - 1)(x + 5) \end{align} $$Vertex form
$$ \begin{align} y = 3(x + 2)^{2} - 27 \end{align} $$Vertex form makes finding the coordinates for the vertex easy. In such an equation the term with the second degree will always be in range such that it is $\ge 0$ or $\le 0$ (it is squared). When the term with the second degree is $0$ the solution that results is the minimum—or maximum—point on the parabola, the vertex.
In the case above we assign $x$ to $-2$ to obtain $0$ for the first term and the minimum value for $y$:
$$ \begin{align} y = 3(x + 2)^{2} - 27\\ y = 3(-2 + 2)^{2} - 27\\ y = 3(0)^{2} - 27\\ y = -27 \end{align} $$So, the coordinates for the vertex are $(-2, 27)$.
Here is an example with a downward opening parabola where the term with the second degree will always be $\le 0$:
$$ \begin{align} y = -2(x - 5)^{2} + 10\\ y = -2(5 - 5)^{2} + 10\\ y = -2(0)^{2} + 10\\ y = -2(0) + 10\\ y = 10 \end{align} $$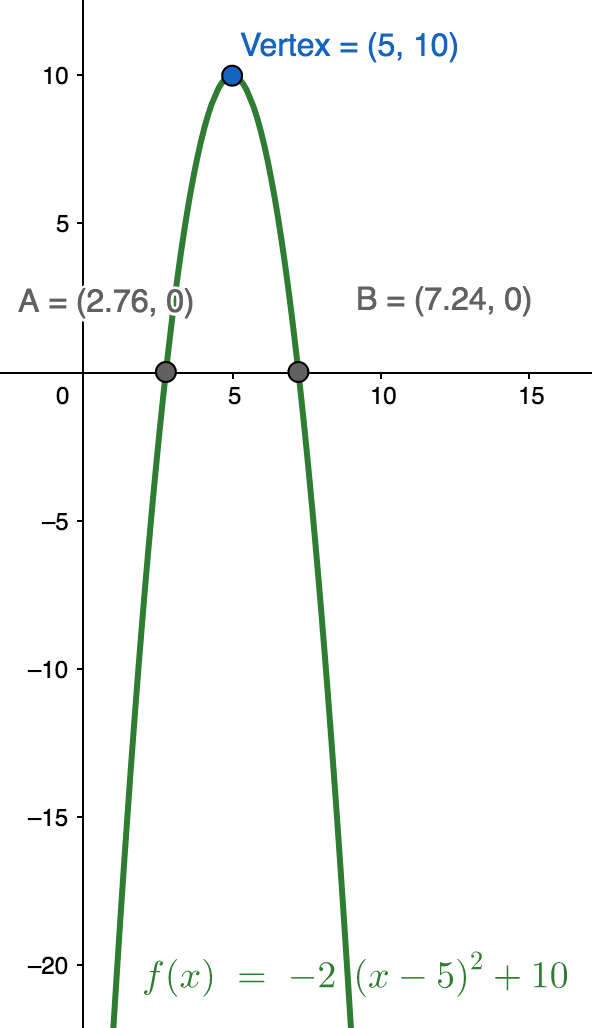
Obtaining the vertex from vertex form is easy even with seemingly complicated equations:
$$ \begin{align} y = \pi(x - 2.8)^{2} + 7.1\\ y = \pi(2.8 - 2.8)^{2} + 7.1\\ y = \pi(0)^{2} + 7.1\\ y = 7.1 \end{align} $$Graphing quadratics: vertex form
Graph the following:
$$ \begin{align} y = -2(x - 2)^{2} + 5 \end{align} $$Note that this is vertex form so we can first solve for the vertex by plugging in a value that will give us the most extreme value possible for $y$:
$$ \begin{align} y = -2(2 - 2)^{2} + 5\\ y = -2(0)^{2} + 5\\ y = 5 \end{align} $$We now know the vertex is at $(2, 5)$.
Now we want to find the points that intersect the $x$-axis for a complete parabola. We now rearrange the equation such that we may unsquare the second degree term:
$$ \begin{align} y = -2(x - 2)^{2} + 5\\ -5 = -2(x - 2)^{2}\\ \frac{5}{2} = (x - 2)^{2}\\ \pm\sqrt{\frac{5}{2}} = x - 2\\ x = 2 + \pm\sqrt{\frac{5}{2}} \end{align} $$Quadratic word problems (vertex form)
An object is launched form a platform.
Its height (in meters), $x$ seconds after the launch, is modeled by:
$$ \begin{align} h(x) = -5(x - 4)^{2} + 180 \end{align} $$How high is the platform?
- this equation is in vertex form
- a negative coefficient for the second degree term tells us that the parabola will open downward
The height of the platform is the height of the object at $0$ seconds or $h(0)$.
Plugging $0$ in for $x$ gives us the answer:
$$ \begin{align} -5(0 - 4)^{2} + 180\\ -5(-4)^{2} + 180\\ -5 \cdot 16 + 180\\ -80 + 180\\ 100 \end{align} $$Next, when do we hit the maximum height i.e. the vertex?
In order to get the maximum value, the non-constant term will need to be resolve to $0$.
Plugging in $4$ for $x$ gives us the maximum value of $180$. So, we know that at $4$ seconds the object will be at its maximum height.
Lastly, when does the height reach $0$ i.e. the object hits the ground. We can solve this by finding the $x$s.
First, we substitute in $0$.
$$ \begin{align} -5(x - 4)^{2} + 180 = 0\\ -5(x - 4)^{2} = -180\\ -5(x - 4)^{2} = -180\\ (x - 4)^{2} = 36\\ x - 4 = \pm 6\\ x = \pm 6 + 4 \end{align} $$$x = -2$ or $x = 10$. We know that time cannot be negative, so the answer is $10$ seconds.
Solving quadratics by factoring
Solving quadratics by factoring (example)
Solve:
$$ \begin{align} s^{2} - 2s - 35 = 0\\ \end{align} $$First, factor:
$$ \begin{align} (s - 7)(s + 5) = 0 \end{align} $$Then find two instances where the equation can be satisfied:
$$ \begin{align} s = 7 \text{and} s = -5 \end{align} $$Solving quadratics by factoring (article)
Solving factored quadratic equations
Suppose we are asked to solve the quadratic equation $(x - 1)(x + 3) = 0$.
Note that any $x$ value that makes either $(x - 1)$ or $(x + 3)$ zero, will make their product zero.
$$ \begin{align} x - 1 = 0 \\ x = 1\\ x + 3 = 0\\ x = -3 \end{align} $$A note about the zero-product property
How do we know there are no more solutions other than the two we find using our method?
The answer is provided by… the zero-product property:
If the product of two quantities is equal to zero, then at least one of the quantities must be equal to zero.
Solving quadratics by factoring: leading coefficient $\ne 1$
Solve:
$$ \begin{align} 6x^{2} - 120x + 600 = 0\\ 6(x^{2} - 20x + 100) = 0\\ (x - 10)^{2} = 0\\ \end{align} $$Since there is only one value for $x$ which satisfies this equation, we know that $x$ is $10$
Solving quadratics using structure
Solve
$$ \begin{align} (2x - 3)^{2} = 4x - 6\\ (2x - 3)(2x - 3) = 2(2x - 3)\\ \end{align} $$We will now substitute in $p$ for $(2x - 3)$:
$$ \begin{align} p^{2} = 2p\\ p^{2} - 2p = 0\\ p(p - 2) = 0\\ p = 0 \text{and} p = 2 \end{align} $$Next, we’ll substitute $p$ back into the original equation:
$$ \begin{align} 2x - 3 = 0\\ 2x = 3\\ x = \frac{2}{3}\\ \text{or}\\ 2x - 3 = 2\\ 2x = 5\\ x = \frac{5}{2} \end{align} $$Quadratic equations word problem: triangle dimensions
The height of a triangle is $4$ inches less than the length of the base. The area of the triangle is $30\text{in}^{2}$. Find the height and base.
Use the formula $A = \frac{1}{2}bh$ for the area of a triangle.
$$ \begin{align} \frac{1}{2}bh = 30\\ \frac{1}{2}(b \cdot (b -4)) = 30\\ (b \cdot (b - 4)) = 60\\ b^{2} - 4b = 60\\ b^{2} - 4b - 60 = 0\\ (b - 10)(b + 6) = 0 \end{align} $$We have two solutions:
$$ \begin{align} b = 10\\ \text{and}\\ b = -6 \end{align} $$A triangle cannot have a negative base/height, so the base and height are as follows:
$$ \begin{align} b = 10, h = 6\\ \end{align} $$Quadratic equations word problem: box dimensions
The volume of a box is $405$ cube units.
The length is $x$ units, the width is $x + 4$ units, and the height is $9$ units. In units, what are the dimensions of the box?
$$ \begin{align} 405 = x \cdot (x + 4) \cdot 9\\ 405 = x^{2} + 4x \cdot 9\\ 45 = x^{2} + 4x\\ 0 = x^{2} + 4x - 45\\ 0 = (x + 9)(x - 5) \end{align} $$$x$ cannot be negative so $x$ must be $5$, so:
$$ \begin{align} \text{length} = 5\\ \text{width} = 9\\ \text{height} = 9 \end{align} $$Solving quadratics by factoring review
Completing the square
Completing the square (intro)
Solving quadratics by completing the square
What you will learn in this lesson
So far, you’ve either solved quadratic equations by taking the square root or by factoring. These methods… are not always applicable.
In this lesson, you will learn a method for solving any kind of quadratic equation.
Solving quadratic equations by completing the square (example)
Example:
$$ \begin{align} x^{2} + 6x = -2 x^{2} + 6x + 9 = -2 + 9\\ (x +3)^{2} = 7\\ x + 3 = \pm \sqrt{7} x = \pm \sqrt{7} - 3 \end{align} $$What happened here?
Adding $9$ to $x^{2} + 6x$ had the fortunate result of making the expression a perfect square that can be factored as $(x + 3)^{2}$. This allowed us to solve the equation by taking the square root.
How to complete the square
To understand why $9$ was chosen, we should ask ourselves the following question: If $x^{2} + 6x$ is the beginning of a perfect square expression, what should be the constant term?
Let’s assume that the expression can be factored as the perfect square $(x + a)^{2}$ where the value of constant $a$ is still unknown. This expression is expanded as $x^{2} + 2ax + a^{2}$, which tells us two things:
- The coefficient of $x$, which we know to be $6$, should be equal to $2a$. This means that $a = 3$.
- The constant number we need to add is equal to $a^{2}$, which is $3^{2} = 9$.
[Shortcut:]
[I]n order to complete $x^{2} + bx$ into a perfect square, where $b$ is any number, we need to add $(\frac{b}{2})^{2}$ to it.
For example, in order to complete $x^{2} + 6x$ into a perfect square, we added $(\frac{6}{2})^{2} = 9$ to it.
Arranging the equation before completing the square
Rule 1: Separate the variable terms from the constant term
This is how the solution of the equation $x^{2} + 5x - 6 = x + 1$ goes:
$$ \begin{align} x^{2} + 5x - 6 = x + 1\\ x^{2} + 4x - 6 = 1\\ x^{2} + 4x = 7\\ x^{2} + 4x + 4 = 7 + 4\\ (x + 2)^{2} = 11\\ x + 2 = \pm \sqrt{11}\\ x = \pm \sqrt{1} - 2 \end{align} $$Rule 2: Make sure the coefficient of $x^{2}$ is equal to $1$
This is how the solution of the equation $3x^{2} - 36x = -42$ goes:
$$ \begin{align} 3x^{2} - 36x = -42\\ x^{2} - 12x = -14\\ x^{2} - 12x + 36 = 36 - 14\\ (x - 6)^{2} = 22\\ x - 6 = \pm \sqrt{22}\\ x = \pm \sqrt{22} + 6 \end{align} $$Worked example: Completing the square (intro)
Use completing the square to find the value of $c$ that makes $x^{2} - 44x + c$ a perfect square trinomial. Then write the expression as the square of a binomial.
First reflect on the following:
$$ \begin{align} (x + a)^{2} = (x + a)(x + a) =\\ x^{2} + ax + ax + a^{2} =\\ x^{2} + 2ax + a^{2} \end{align} $$We can determine that:
$$ \begin{align} 2a = -44\\ a = -22\\ a^{2} = 484 = c \end{align} $$$$ \begin{align} x^{2} - 44x + 484 =\\ (x - 22)^{2} \end{align} $$Worked example: Rewriting expressions by completing the square
Rewrite the following in the form $(x + a)^{2} + b$:
$$ \begin{align} x^{2} + 16x + 9 \end{align} $$We can expand $(x + a)^{2} + b$:
$$ \begin{align} x^{2} + 2ax + a^{2} + b \end{align} $$And, use this pattern with our original equation:
$$ \begin{align} x^{2} + 2(8)x + 64 + 9 - 64 \end{align} $$($64$ must be subtracted since it is added)
Now, the first part of the equation follows the pattern of a perfect square quadratic.
($x^{2} + 16x + 64$)
We can use the information to fill in the pattern $(x + a)^{2} + b$, thus completing the square:
$$ \begin{align} (x + 8)^{2} - 55 \end{align} $$Worked example: Solving equations by completing the square
Complete the square for:
$$ \begin{align} x^{2} - 2x - 8 = 0 \end{align} $$In other words, we are seeking to rewrite the formula in the format $(x + a)^{2} + b$.
Recall that this can be rewritten as $x^{2} + 2ax + a^{2} + b$, and first we will use this as the pattern for the original equation.
$2ax = -2x$, and thus, $a = -1$. We can now determine that $a^{2}$, but if we add $1$ we must also subtract it. Now, we can find the solution:
$$ \begin{align} x^{2} - 2x + 1 - 1 - 8 = 0\\ (x - 1)^{2} - 9 = 0\\ (x - 1)^{2} = 9\\ x - 1 = \pm 3\\ x = \pm 3 + 1 \end{align} $$Worked example: completing the square (leading coefficient $\ne 1$
Solve:
$$ \begin{align} 4x^{2} + 40x - 300 = 0 \end{align} $$First, we can divide both sides by $4$ (yes, we really can do that):
$$ \begin{align} x^{2} + 10x - 75 = 0 \end{align} $$We now must complete the square:
$$ \begin{align} x^{2} + 10x + 25 - 75 - 25 = 0 \end{align} $$$$ \begin{align} (x + 5)^{2} - 100 = 0\\ (x + 5)^{2} = 100\\ x + 5 = \pm 10\\ x = \pm 10 - 5\\ x = 5 \text{and} x = -15 \end{align} $$Solving quadratics by completing the square: no solution
Use completing the square to find the roots (find $x$ where $y = 0$) of the quadratic equation:
$$ \begin{align} y = 4x^{2} + 40x + 280 \end{align} $$First, assign $y$ to $0$:
$$ \begin{align} 0 = 4x^{2} + 40x + 280 \end{align} $$Then, continue:
$$ \begin{align} 0 = 4(x^{2} + 10x + 70)\\ 0 = x^{2} + 10x + 70\\ 0 = x^{2} + 10x + 25 + 70 - 25\\ 0 = (x + 5)^{2} + 45\\ -45 = (x + 5)^{2} \end{align} $$Now, you can see that there can be no solution as you cannot unsquare a negative number. If we assume $x$ is a real number there is no way to satisfy this equation.
Quadratic standard form
Finding the vertex of a parabola in standard form
Given the quadratic equation $5x^{2} - 20x + 15$ we want to find the vertex.
It turns out that we are able to find the $x$-vertex using the formula $\frac{-b}{2a}$:
$$ \begin{align} \frac{-(-20)}{2 \cdot 5} = 2 \end{align} $$We can find the $y$-value for the vertex by substituting back in the value for $x$ in the original equation:
$$ \begin{align} 5 \cdot -5^{2} -20(5) + 15 = -5 \end{align} $$The coordinates for the vertex are $(2, -5)$
We can double check this by completing the square:
$$ \begin{align} y = 5(x^{2} - 4x) + 15\\ y = 5(x^{2} - 4x + 4) + 15 -20\\ y = 5(x - 2)^{2} - 5 \end{align} $$We will hit a minimum value when $y = -5$ and $x = 2$—where the result of $5(x - 2)^{2}$.
Graphing quadratics standard form
Graph $y = 5x^{2} - 20x + 15$.
You can graph such an equation with 3 values for $x$. Another convention is to find the vertex, and two points where the parabola intersects the $x$-axis.
Let’s determine where the parabola crosses $x$-axis by setting $y$ to $0$:
$$ \begin{align} 0 = 5x^{2} - 20x + 15\\ 0 = x^{2} - 4x + 3\\ 0 = (x - 3)(x - 1) \end{align} $$In this case $y$ is $0$ when $x = 3$ and $x = 1$.
The vertex is halfway between these two values so the $x$ value is $2$.
We can plug in $x$ to get the $y$ value:
$$ \begin{align} y = 5(2)^{2} -20(2) + 15\\ y = 20 - 40 + 15\\ y = -5 \end{align} $$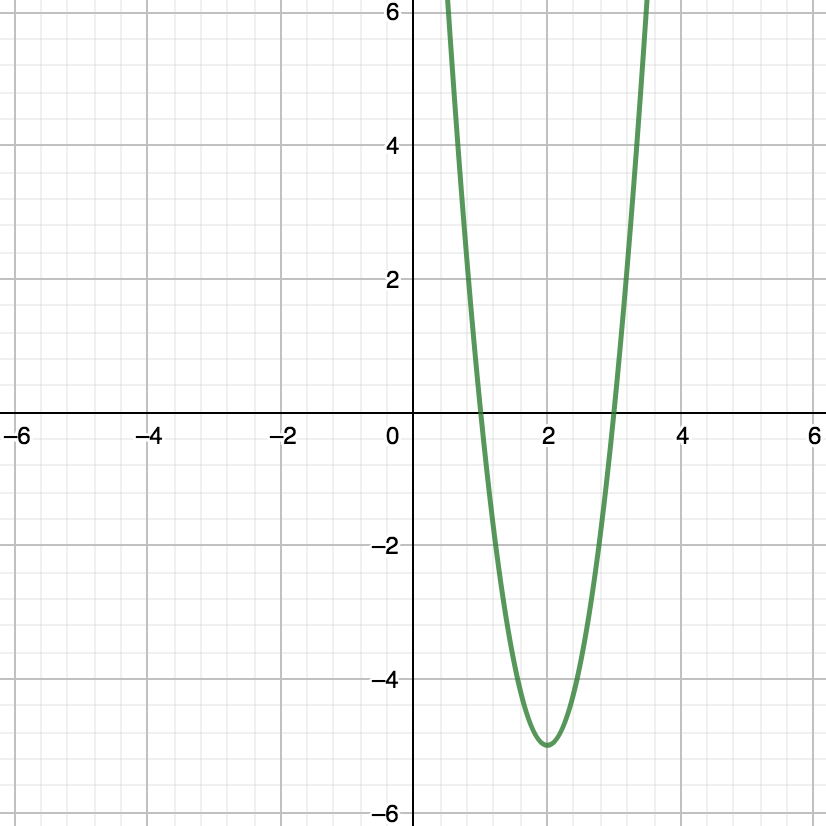
Quadratic word problem: ball
A ball is shot into the air from the edge of a building, 50 feet above the ground. Its initial velocity is 20 feet per second.
The equation $h = -16t^{2} + 20t + 50$ can be used to model the height of the ball after $t$ seconds. About how long does it take for the ball to hit the ground.
If $y$-axis is height then we know that the ground is where the parabola crosses the $x$-axis. In other words we want the greater $x$-value where the $y$-value is $0$.
First, we’ll factor out $-2$ from the original equation, making $a$ positive in the process:
$$ \begin{align} h = -2(8t^{2} - 10t - 25) h = 8t^{2} - 10t - 25 \end{align} $$Now, we’ll plug in the appropriate values to solve for $x$ using the quadratic equation:
$$ \begin{align} t = \frac{-(-10) \pm \sqrt{-10^{2} - 4(8)(-25)}}{2(8)}\\ t = \frac{-10 \pm \sqrt{100 + 800}}{-32}\\ t = \frac{-10 \pm 300}{-32}\\ t = \frac{-5 \pm 150}{-16}\\ \end{align} $$$t = 20$ and $t = \frac{145}{8}$
Forms & features of quadratic functions
Forms & features of quadratic functions (intro)
Worked examples: Forms & features of quadratic functions
Vertex & axis of symmetry of a parabola
Finding features of quadratic functions
Comparing features of quadratic functions
Comparing maximum points of quadratic functions
Transforming parabolas
Intro to parabola transformations
How can we go about transforming the given parabola for $y = x^{2}$?

- $y = 2x^{2}$ results in a steeper parabola with respect to $y = x^{2}$.
- $y = \frac{1}{2}x^{2} gives a less steep parabola with respect to $y = x^{2}$.
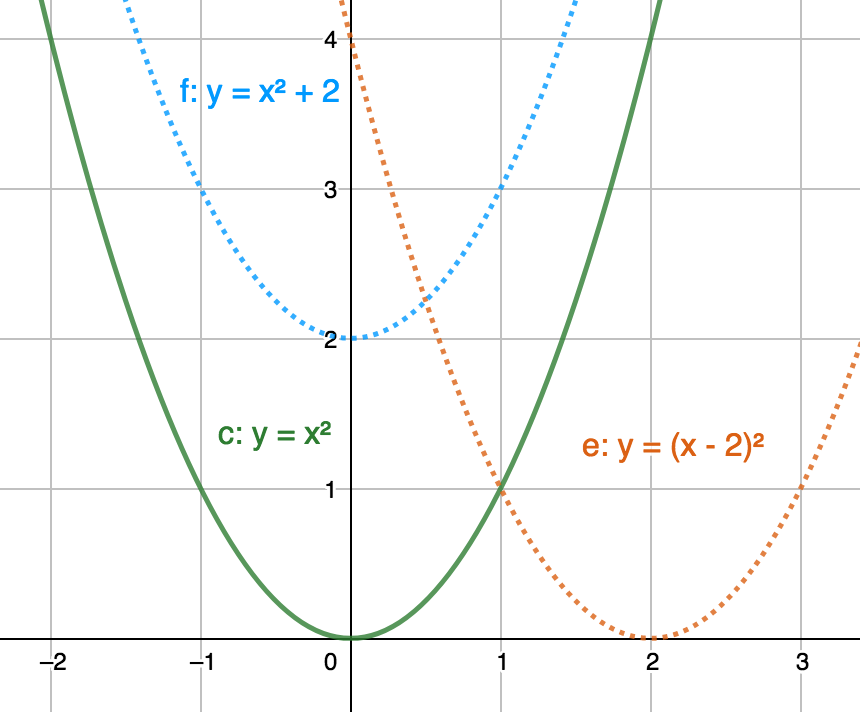
- $y = x^{2} + 2$ results in a vertical transformation upward.
- $y = (x - 2)^{2}$ results in a horizontal transformation to the right.
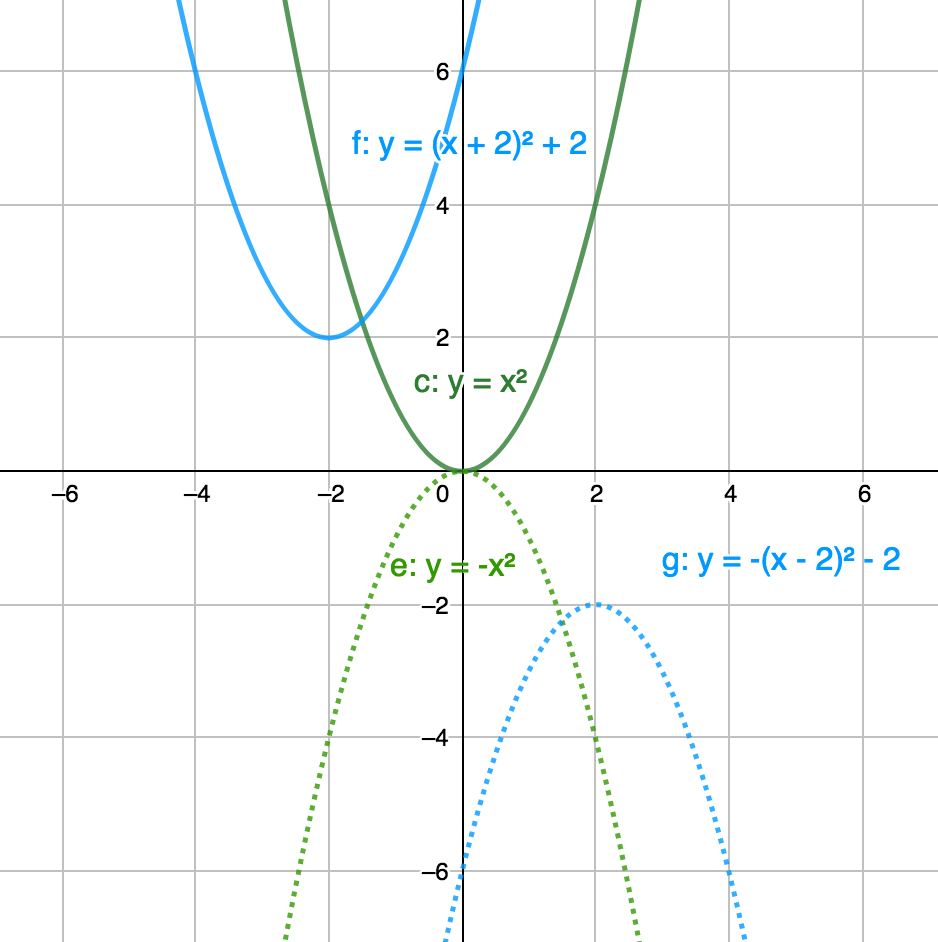
- $y = -x^{2}$ results in a mirror image of $y = x^{2}$.
- $y = -(x - 2)^{2} - 2$ mirrors $y = (x + 2)^{2} + 2$ vertically and horizontally.
Shifting parabolas
How can we shift $y = x^{2}$ to get $e$?
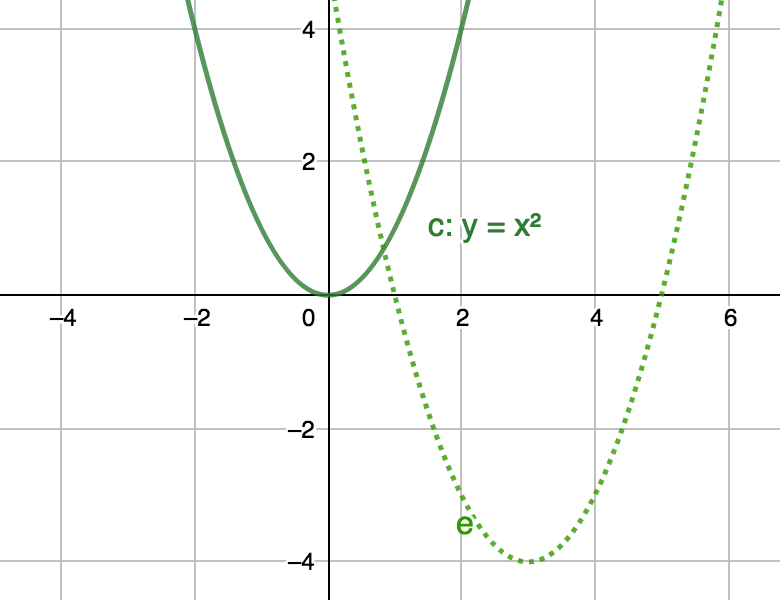
- First, we can shift to the right by subtracting three from $x$ as in $y = (x - 3)^{2}$. This seems counter-intuitive but consider that in order to get $0$ for $y$ (intercept the $y$-axis) we need to subtract $3$ from $x$.
- Next, we can shift down by $4$ by subtracting $4$ as in $y = (x - 3)^{2} - 4$. More intuitively, we are shifting the resultant value by $4$ that would otherwise be $0$ when $x$ is $3$.
Scaling & reflecting parabolas
How can we scale and reflect $y = x^{2}$ to get $e$?
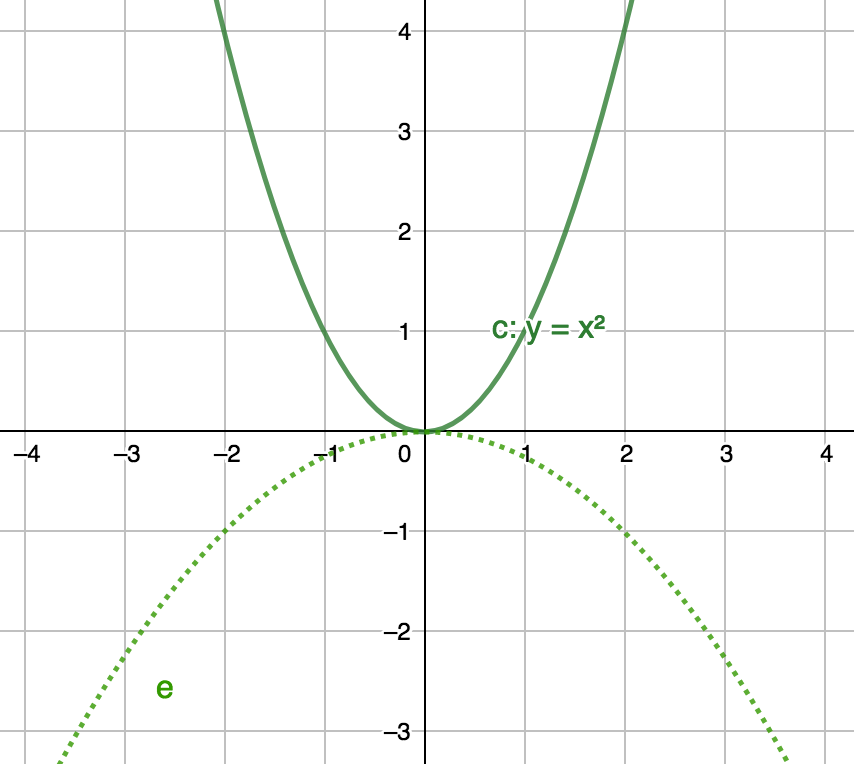
- First, we can reflect the parabola by making the coefficient for the 2nd degree term negative as in $y = -x^{2}$.
- Next, we can scale the parabola by changing the value of the coefficient for the 2nd degree term as in $y = -\frac{1}{4}x^{2}$. This is easily done by picking transforming a point on a reflected version of $y = x^{2}$. For example $(2, -1)$ on $e$ is $\frac{1}{4}\text{th}$ the height of $(2, -4)$ on a reflection of $y = x^{2}$ i.e. $y = -x^{2}$.
Quadratics - revised
Example Problems
Determining the Vertex
Determining the vertex using $x$-intercepts
Given the following quadratic equation what are the coordinates of the vertex?
$$ \begin{align} y = \frac{1}{2}(x - 6)(x + 2) \end{align} $$First, we’ll solve where $x = 0$ as this tells us where the parabola intersects the $x$-axis:
$$ \begin{align} \frac{1}{2}(x - 6)(x + 2) = 0 \end{align} $$$x$ is $0$ when $x - 6 = 0$ or $x + 2 = 0$
We determine that:
$$ \begin{align} x = 6 \end{align} $$$$ \begin{align} x = -2 \end{align} $$Since the vertex lies between these two values for $x$, we can determine the $x$ value for the vertex to be:
$$ \begin{align} 6 + (-2) / 2 = 2 \end{align} $$Since the vertex lies on the axis of symmetry—exactly between the $x$-intercepts—the $x$-value for the vertex is the mean of the two $x$ coordiates of the $x$-intercepts (if there are 2).
Determining the vertex using the quadratic formula
Given the quadratic equation $5x^{2} - 20x + 15$ we want to find the vertex.
It turns out that we are able to find the $x$-vertex using the formula $\frac{-b}{2a} (a component of the quadratic formula)$:
$$ \begin{align} \frac{-(-20)}{2 \cdot 5} = 2 \end{align} $$We can find the $y$-value for the vertex by substituting back in the value for $x$ in the original equation:
$$ \begin{align} 5 \cdot -5^{2} -20(5) + 15 = -5 \end{align} $$The coordinates for the vertex are $(2, -5)$
Note that this strategy is needed when the parabola does not intersect the $x$-axis two times.
Transforming Parabolas
How can we go about transforming the given parabola for $y = x^{2}$?

- $y = 2x^{2}$ results in a steeper parabola with respect to $y = x^{2}$.
- $y = \frac{1}{2}x^{2} gives a less steep parabola with respect to $y = x^{2}$.

- $y = x^{2} + 2$ results in a vertical transformation upward.
- $y = (x - 2)^{2}$ results in a horizontal transformation to the right.

- $y = -x^{2}$ results in a mirror image of $y = x^{2}$.
- $y = -(x - 2)^{2} - 2$ mirrors $y = (x + 2)^{2} + 2$ vertically and horizontally.
Shifting parabolas
How can we shift $y = x^{2}$ to get $e$?

- First, we can shift to the right by subtracting three from $x$ as in $y = (x - 3)^{2}$. This seems counter-intuitive but consider that in order to get $0$ for $y$ (intercept the $y$-axis) we need to subtract $3$ from $x$.
- Next, we can shift down by $4$ by subtracting $4$ as in $y = (x - 3)^{2} - 4$. More intuitively, we are shifting the resultant value by $4$ that would otherwise be $0$ when $x$ is $3$.
Scaling & reflecting parabolas
How can we scale and reflect $y = x^{2}$ to get $e$?

- First, we can reflect the parabola by making the coefficient for the 2nd degree term negative as in $y = -x^{2}$.
- Next, we can scale the parabola by changing the value of the coefficient for the 2nd degree term as in $y = -\frac{1}{4}x^{2}$. This is easily done by picking transforming a point on a reflected version of $y = x^{2}$. For example $(2, -1)$ on $e$ is $\frac{1}{4}\text{th}$ the height of $(2, -4)$ on a reflection of $y = x^{2}$ i.e. $y = -x^{2}$.
Graphing Quadratic Equations
Graphing quadratics in factored form
Graph:
$$ \begin{align} y = \frac{1}{2}(x - 6)(x + 2) \end{align} $$The key insight is that you’ll get a quadratic by multiplying this out, and that it is a parabola.
First, we’ll solve where $x = 0$ as this tells us where the parabola intersects the $x$-axis:
$$ \begin{align} \frac{1}{2}(x - 6)(x + 2) = 0 \end{align} $$$x$ is $0$ when $x - 6 = 0$ or $x + 2 = 0$
We determine that:
$$ \begin{align} x = 6 \end{align} $$$$ \begin{align} x = -2 \end{align} $$Since the vertex lies between these two values for $x$, we can determine the $x$ value for the vertex to be:
$$ \begin{align} 6 + (-2) / 2 = 2 \end{align} $$Plugging this value into our original equation as $x$ gives us the $y$ value for the vertex:
$$ \begin{align} y = \frac{1}{2}(2 - 6)(2 + 2) =\\ \frac{1}{2}(-4)(4) =\\ \frac{1}{2}(-16) =\\ -8 \end{align} $$
Graphing quadratics: vertex form
Graph the following:
$$ \begin{align} y = -2(x - 2)^{2} + 5 \end{align} $$Note that this is vertex form so we can first solve for the vertex by plugging in a value that will give us the most extreme value possible for $y$:
$$ \begin{align} y = -2(2 - 2)^{2} + 5\\ y = -2(0)^{2} + 5\\ y = 5 \end{align} $$We now know the vertex is at $(2, 5)$.
Now we want to find the points that intersect the $x$-axis for a complete parabola. We now rearrange the equation such that we may unsquare the second degree term:
$$ \begin{align} y = -2(x - 2)^{2} + 5\\ -5 = -2(x - 2)^{2}\\ \frac{5}{2} = (x - 2)^{2}\\ \pm\sqrt{\frac{5}{2}} = x - 2\\ x = 2 + \pm\sqrt{\frac{5}{2}} \end{align} $$Graphing quadratics standard form
Graph $y = 5x^{2} - 20x + 15$.
You can graph such an equation with 3 values for $x$. Another convention is to find the vertex, and two points where the parabola intersects the $x$-axis.
Let’s determine where the parabola crosses $x$-axis by setting $y$ to $0$:
$$ \begin{align} 0 = 5x^{2} - 20x + 15\\ 0 = x^{2} - 4x + 3\\ 0 = (x - 3)(x - 1) \end{align} $$In this case $y$ is $0$ when $x = 3$ and $x = 1$.
The vertex is halfway between these two values so the $x$ value is $2$.
We can plug in $x$ to get the $y$ value:
$$ \begin{align} y = 5(2)^{2} -20(2) + 15\\ y = 20 - 40 + 15\\ y = -5 \end{align} $$
Word Problems
Quadratic word problems (factored form)
A rocket is launched from a platform. Its height (in meters), $x$ seconds after the launch, is modeled by
$$ \begin{align} h(x) = -4(x + 2)(x - 18) \end{align} $$What is the height of the rocket at the time of launch?
The time of launch is $0$ seconds. We can plug that in right away to obtain the $y$-value (height):
$$ \begin{align} -4(0 + 2)(0 - 18) =\\ 144 \end{align} $$How many seconds after launch will the rocket hit the ground?
Let’s find the two $x$-intercepts—the higher of the two will represent the time when the rocket hits the ground (0 meters):
$$ \begin{align} x + 2 = 0\\ x = -2 \end{align} $$And
$$ \begin{align} x - 18 = 0\\ x = 18 \end{align} $$How many seconds after being launched will the rocket reach its maximum height?
The parabola will have the highest $y$-value exactly between the $x$-intercepts (the axis of symmetry):
$$ \begin{align} (-2 + 18)/ 2 =\\ 16/2 = 8 \end{align} $$What is the maximum height that the rocket will reach?
We can find this with the $x$-value for the axis of symmetry:
$$ \begin{align} -4(8 + 2)(8 - 18) =\\ -4(10)(-10) =\\ 400 \end{align} $$Quadratic equations word problem: triangle dimensions
The height of a triangle is $4$ inches less than the length of the base. The area of the triangle is $30\text{in}^{2}$. Find the height and base.
Use the formula $A = \frac{1}{2}bh$ for the area of a triangle.
$$ \begin{align} \frac{1}{2}bh = 30\\ \frac{1}{2}(b \cdot (b -4)) = 30\\ (b \cdot (b - 4)) = 60\\ b^{2} - 4b = 60\\ b^{2} - 4b - 60 = 0\\ (b - 10)(b + 6) = 0 \end{align} $$We have two solutions:
$$ \begin{align} b = 10\\ \text{and}\\ b = -6 \end{align} $$A triangle cannot have a negative base/height, so the base and height are as follows:
$$ \begin{align} b = 10, h = 6\\ \end{align} $$Quadratic equations word problem: box dimensions
The volume of a box is $405$ cube units.
The length is $x$ units, the width is $x + 4$ units, and the height is $9$ units. In units, what are the dimensions of the box?
$$ \begin{align} 405 = x \cdot (x + 4) \cdot 9\\ 405 = x^{2} + 4x \cdot 9\\ 45 = x^{2} + 4x\\ 0 = x^{2} + 4x - 45\\ 0 = (x + 9)(x - 5) \end{align} $$$x$ cannot be negative so $x$ must be $5$, so:
$$ \begin{align} \text{length} = 5\\ \text{width} = 9\\ \text{height} = 9 \end{align} $$Quadratic word problem: ball
A ball is shot into the air from the edge of a building, 50 feet above the ground. Its initial velocity is 20 feet per second.
The equation $h = -16t^{2} + 20t + 50$ can be used to model the height of the ball after $t$ seconds. About how long does it take for the ball to hit the ground.
If $y$-axis is height then we know that the ground is where the parabola crosses the $x$-axis. In other words we want the greater $x$-value where the $y$-value is $0$.
First, we’ll factor out $-2$ from the original equation, making $a$ positive in the process:
$$ \begin{align} h = -2(8t^{2} - 10t - 25) h = 8t^{2} - 10t - 25 \end{align} $$Now, we’ll plug in the appropriate values to solve for $x$ using the quadratic equation:
$$ \begin{align} t = \frac{-(-10) \pm \sqrt{-10^{2} - 4(8)(-25)}}{2(8)}\\ t = \frac{-10 \pm \sqrt{100 + 800}}{-32}\\ t = \frac{-10 \pm 300}{-32}\\ t = \frac{-5 \pm 150}{-16}\\ \end{align} $$$t = 20$ and $t = \frac{145}{8}$