Linear Equations
Overview
A linear equation is named so because if you graph all of the $x$ and $y$ values, you end up with a line. Every term is either a constant e.g. $5$ or a first degree term (raised to the first power) e.g. $5x$ ($5x^{1}$)
Here is a linear equation:
$$ \begin{align} y = 2x - 3 \end{align} $$We can plot $x$ and $y$ values in a table:
+———-+———-+ |x |y | +———-+———-+ |0 |-3 | +———-+———-+ |1 |-1 | +———-+———-+ |2 |1 | +———-+———-+
We can graph a line using these values:
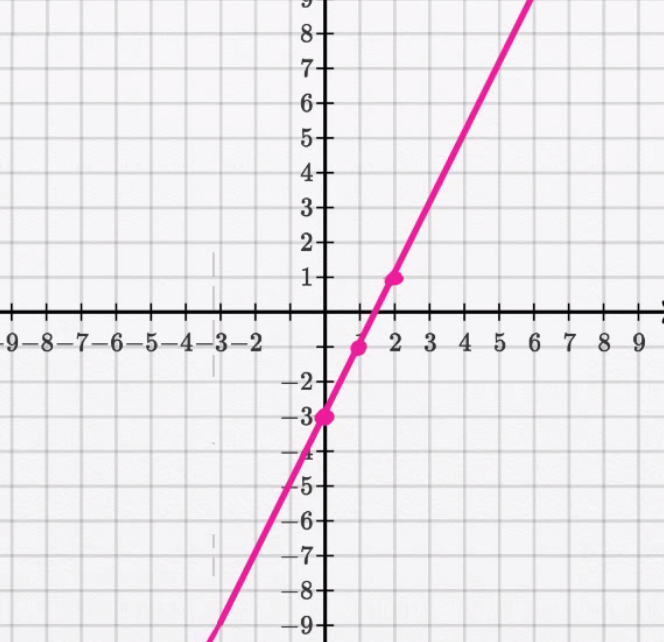
All solutions to the equation are on this same line.
Non-linear equations represent a set of solutions which do not graph on a straight line. Examples include $y = x^{2}$, $xy = 12$, and $\frac{5}{x} + y = 10$.
An x-intercept is a solution for an equation where the $y$ coordinate, or the input value for a function, is $0$. Put another way, it is where a graphed equation intersects the $x$-axis. A y-intercept is a solution for an equation where the $x$ coordinate, or output value for a function, is $0$. Put another way, it is where a graphed equation intersects the $y$-axis.
Given the equation:
$$ \begin{align} y = \frac{1}{2}x - 3 \end{align} $$The $y$-intercept is at $(6, 0)$, and the $y$-intercept is at $(0, -3)$.
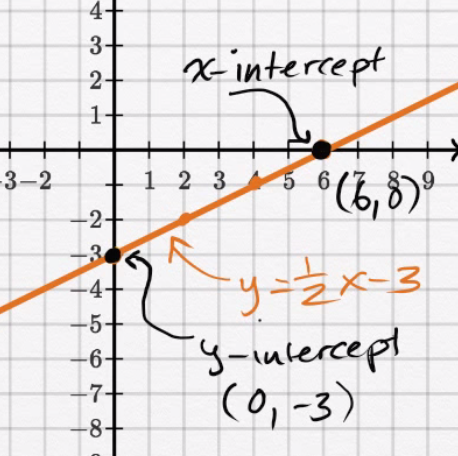
Slope is a number that describes the direction and steepness of a line. More specifically it is a ratio of vertical change to horizontal change in a line.
$$ \begin{align} m = \frac{\Delta y}{\Delta x} = \frac{\text{rise}}{\text{run}} \end{align} $$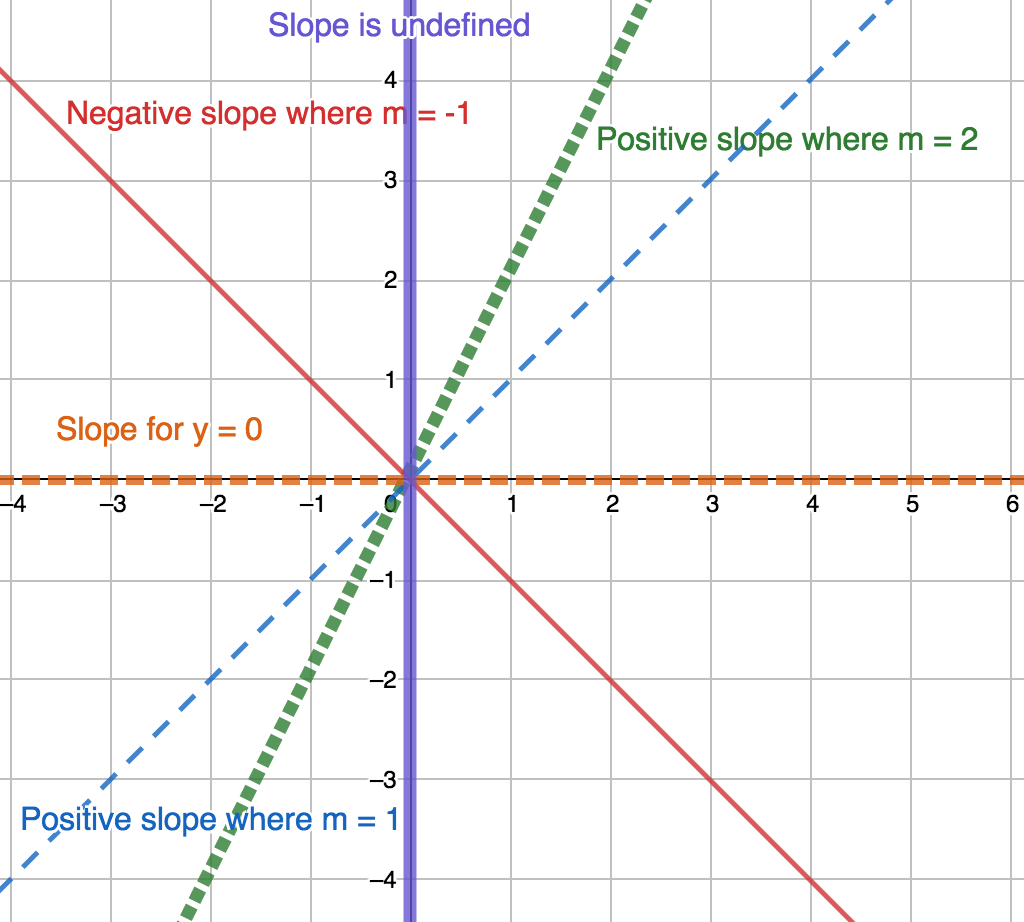
- A negative slope is a negative value and travels down and to the right.
- A positive slope is a positive value and travels up and to the right.
- A slope of $0$ travels from right to left on the same axis.
- An undefined slope travels from top to bottom (you cannot divide by $0$)
We can determine the slope using two ordered pairs from a line with the following equation:
$$ \begin{align} m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \end{align} $$The slope can also be derived with a variation (the values from the second ordered pair are instead subtracted from the first ordered pair):
$$ \begin{align} m = \frac{y_{1} - y_{2}}{x_{1} - x_{2}} \end{align} $$A common way to express a linear equation is slope-intercept form. It is easy to determine the slope and the $y$-intercept with this equation.
$$ \begin{align} y = mx + b \end{align} $$- $m$ is the value for the slope
- $b$ is the value for the $y$-intercept
Example equation:
$$ \begin{align} y = 2x + 4 \end{align} $$point-slope form is a linear equation that is expressed in terms of a slope and two ordered pairs.
Starting with our slope equation we can get to point-slope form:
$$ \begin{align} \frac{y - b}{x - a} = m\\ y - b = m(x - a) \end{align} $$- The first ordered pair is $(a, b)$.
- The second ordered pair is $(x, y)$.
- The slope is $m$.
Given a slope of $m = 2$ and the ordered pair $(-7, 5)$, we can create a point-slope equation of:
$$ \begin{align} y - 5 = 2(x - -7) \end{align} $$This can be modified to be in slope-intercept form:
$$ \begin{align} y - 5 = 2(x - -7)\\ y = 2x + 14 -5\\ y = 2x + 9 \end{align} $$A linear equation standard form is a linear equation that expresses the sum of some $x$ and $y$ pair. It is useful in finding solving systems of two or more linear equations.
It can be written as:
$$ \begin{align} Ax + By = C \end{align} $$A linear equation in standard form:
$$ \begin{align} 9x + 16y = 72 \end{align} $$Graphing on the coordinate plane
2-dimensional coordinate system devised by Rene Descartes.
points are expressed as Cartesian coordinates aka ordered pairs of the form (x, y) where x is the distance from zero on the x axis and y is the distance from zero on the y axis
Axes
All ordered pairs where the value of x is 0 are on the y axis. All ordered pairs where the value of y is 0 are on the x axis.
Quadrants
The coordinate plane is divided into four quadrants.
+x and +y values exist in quadrant I -x and +y values exist in quadrant II -x and -y values exist in quadrant III +x and -y values exist in quadrant IV
Problems
Testing for Solutions
Given the equation:
$$ \begin{align} -3x - y = 6 \end{align} $$Which of the following are solutions: $(-4, 4)$, $(-3, 3)$?
$$ \begin{align} -4(-4) - 4 = 6\\ 16 - 4 = 6\\ 16 \ne 10 \end{align} $$$$ \begin{align} -3(-3) - 3 = 6\\ 9 - 3 = 6\\ 6 = 6 \end{align} $$Only the second pair is a solution.
$x$ and $y$ Intercepts
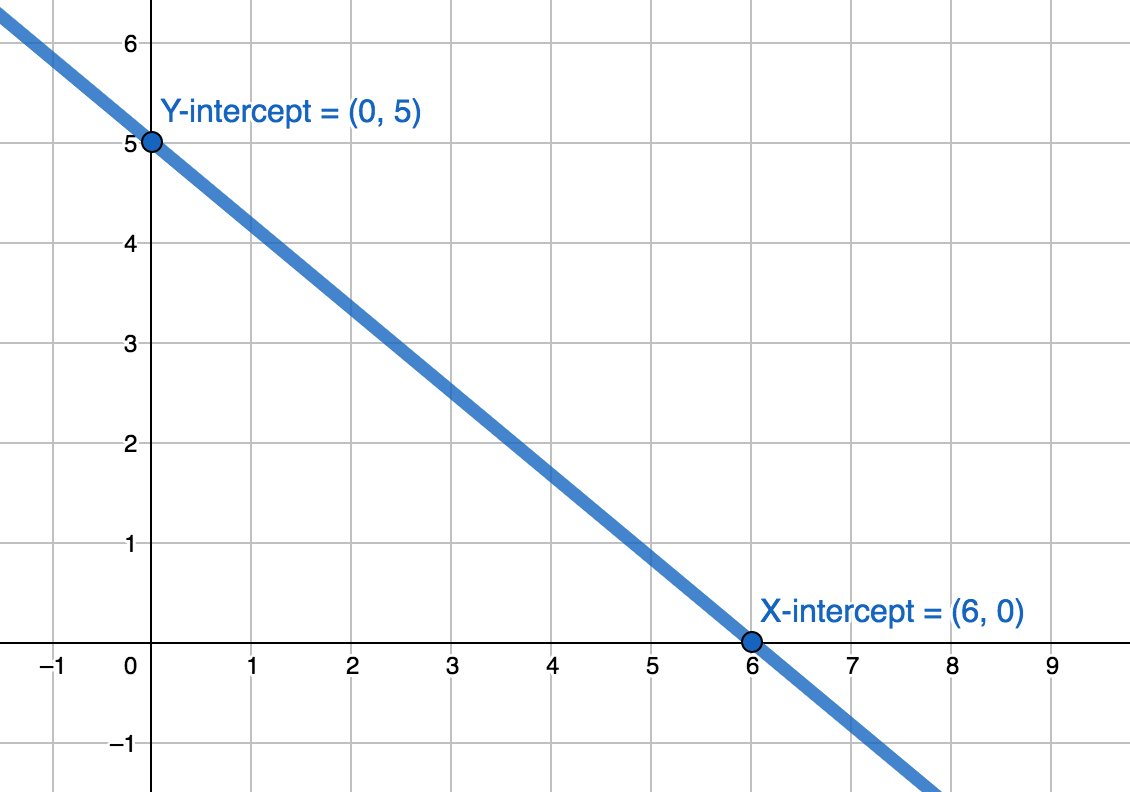
Given the equation:
$$ \begin{align} 5x + 6y = 30 \end{align} $$What are the $x$ and $y$ intercepts and what is the graph for the equation?
We can determine the $x$-intercept by assigning the $y$-coordinate to $0$:
$$ \begin{align} 5x + 6y = 30\\ 5x + 6(0) = 30\\ 5x = 30\\ x = 6 \end{align} $$The $x$-intercept is at $(6, 0)$.
We can determine the $y$-intercept by assinging the $x$-coordinate to $0$:
$$ \begin{align} 5x + 6y = 30\\ 5(0) + 6y = 30\\ 0 + 6y = 30\\ 6y = 30\\ y = 5 \end{align} $$The $y$-intercept is at $(0, 5)$.
Here is the graph of the equation using the two intercepts:
Graphing Equations
Given the equation:
$$ \begin{align} -3x + 7y = 5x + 2y \end{align} $$Find the missing coordinates in the following table, and graph the line:
+———-+———-+ |x |y | +———-+———-+ |-5 |$y_{1}$ | +———-+———-+ |$x_{2}$ |8 | +———-+———-+
First, we can simplify the equation:
$$ \begin{align} -3x + 7y = 5x + 2y\\ 7y = 8x + 2y\\ 5y = 8x\\ y = \frac{8}{5}x \end{align} $$When $x = -5$, $y = -8$, and when $y = 8$, $y = 5$.
We can now graph a line with the two pairs:
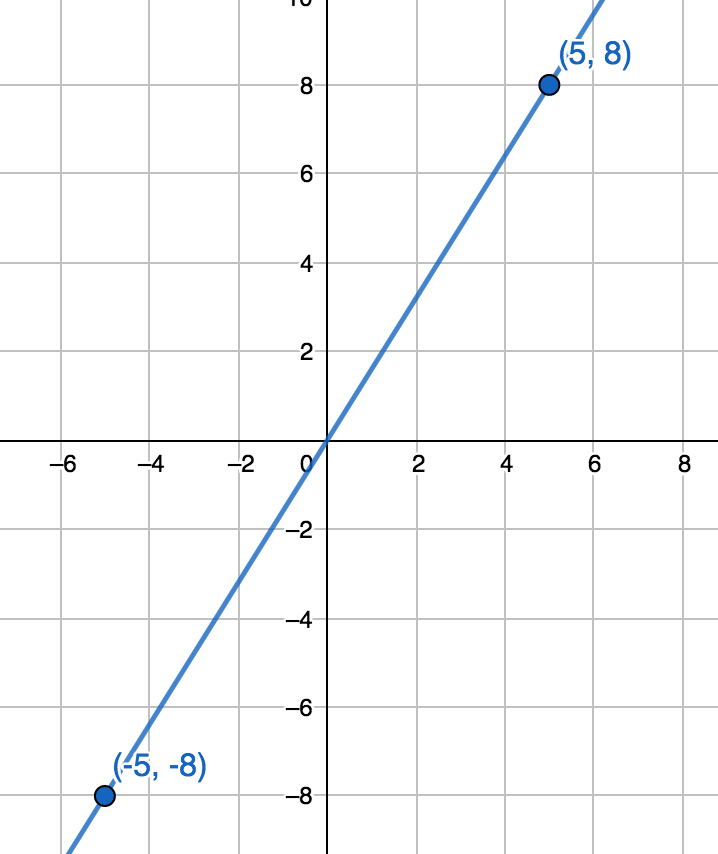
Given the following table, graph the line along with $x$ and $y$ intercepts:
+———-+———-+ |x |y | +———-+———-+ |-2 |8 | +———-+———-+ |1 |2 | +———-+———-+ |2 |0 | +———-+———-+ |4 |-4 | +———-+———-+
The table has provided us with the $x$-intercept of $(2, 0)$.
Now, we need the $y$-intercept.
The important thing to notice from the table is that for every increase in $x$ by $y$ there is a corresponding decrease in $y$ by $2$.
If we “move back” by $1$ from $1$ on the table we get $0$, the corresponding value for the $y$ column (an increase of 2) gives us $4$.
The $y$-intercept is at $(0, 4)$

Finding Slope
Find the slope for the following graph:

We can observe that in going from point $A$ to point $B$ results in the following:
- a change in $x$ of $1$
- a change in $y$ of $3$
We can obtain the slope with the change in $y$ over the change in $x$: $\frac{3}{1}$.
Find the slope of a line that goes through the ordered pairs $(4, 2)$ and $(-3, 16)$.
We can solve using one of our equations for slope:
$$ \begin{align} m = \frac{16 - 2}{-3 - 4}\\ = \frac{14}{-7}\\ = -2 \end{align} $$The slope is downward and has a value of $-2$.
What is the slope of a line whose equation is $y = -1$?

No matter the value of $x$, $y$ does not change. Therefore the slope is $\frac{0}{\Delta x}$, or $0$.
What is the slope of a line whose equation is $x = -1$.

There is no change in $x$ i.e. our slope is $\frac{\Delta y}{0}$. We can divide by $0$—the slope is undefined.
What is the equation of a vertical line through $(-5, -2)$?
Such an equation has no change $x$, and can be expressed as $x = -5$.
What is the equation of a horizontal line through $(1, 9)$?
Such an equation has no change in $y$, and can be expressed as $y = 9$
What is the slope of the following line?
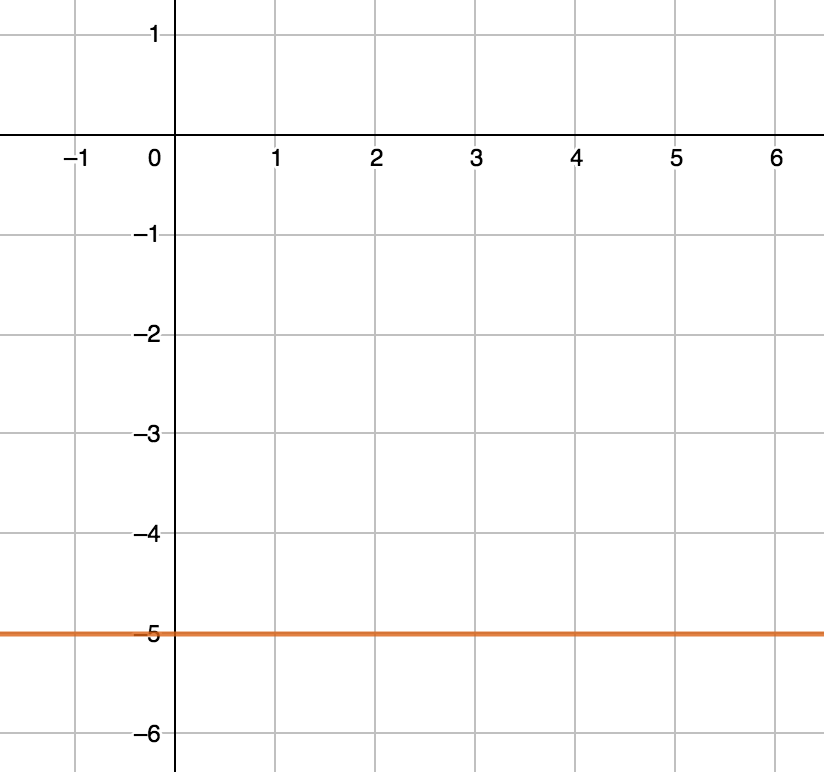
The slope of the line is $0$ as there is no change in $y$ for any change in $x$.
What is the slope of the following line?
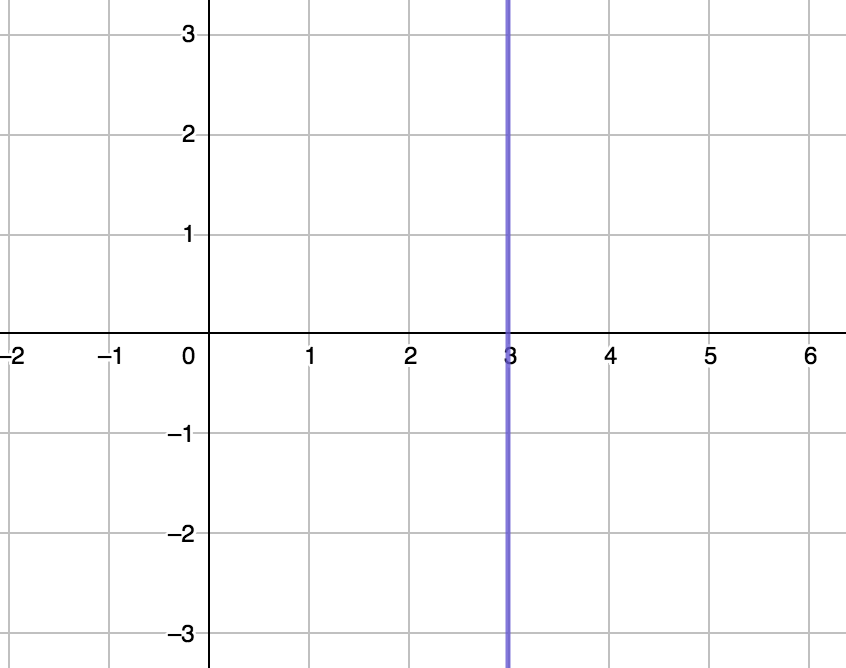
The slope of the line is “undefined” since no matter the change in $y$ there is no change in $0$. $\frac{\Delta y}{0}$ is “undefined”.
What is the slope of $y = -3x - 2$?
$-\frac{3}{1}$ or $-3$.
Slope-Intercept Form
Graph the following equation:
$$ \begin{align} y = \frac{1}{3}x - 2 \end{align} $$We can graph the line by plotting two different points, and then plotting the line that intersects both points
- just by looking at the equation we can determine the $y$-intercept to be $(0, -2)$
- the slope is $\frac{1}{3}$, so we can obtain a second point by going up $1$ (rise) and $3$ over (run) got $(3, -1)$.

Complete the equation of the line whose slope is $5$ and $y$-intercept is $(0, 4)$.
$$ \begin{align} y = 5x + 4 \end{align} $$Determine the equations in slope-intercept form for the following lines:
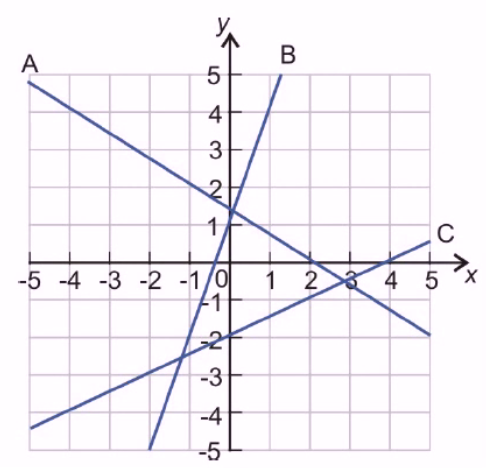
For line A We can discern a slope of $\frac{-2}{3}$ between points $(-1, 2)$ and $(2, 0)$.
By going $1$ over we can obtain the $y$-intercept. By doing this we are travelling $\frac{1}{3}$ the distance of $2$. Subtracting $\frac{1}{3}$ from $2$ gives us $\frac{4}{3}$. Our $y$-intercept is therefore $(0, \frac{4}{3})$.
The equation is therefore $y = \frac{-2}{3}x + \frac{4}{3}$.
Line B intersects the $y$-axis at $1$ so our $y$-intercept is $(0, 1)$. We can discern a slope of $\frac{3}{1}$ between points $(-1, -2)$ and $(0, 1)$. The equation is therefore $y = 3x + 1$.
Line C intersects the $y$-axis at $-2$ so our $y$-intercept is $(0, -2)$. We can discern a slope of $\frac{2}{4}$ between points $(-2, 0)$ and $(0, 4)$. The equation is therefore $y = \frac{1}{2}x - 2$.
Determine the equation for the following graphed line:
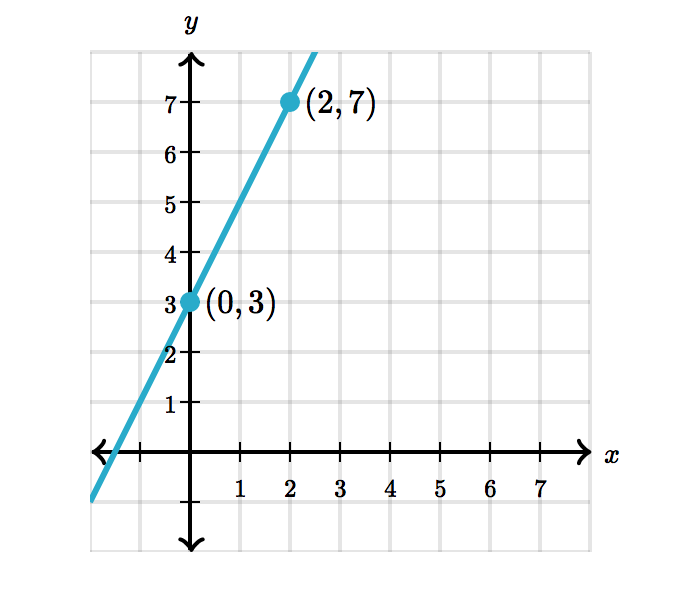
We can see that the $y$-intercept is at $(0, 3)$. We can determine visually that the slope is $2$
Our final equation is therefore $y = 2x + 3$.
A line has a slope of $-\frac{3}{4}$ and goes through the point $(0, 8)$. What is the equation of this line, in slope-intercept form?
Given this information, the equation is $y = -\frac{3}{4}x + 8$.
A line goes through the points $(-1, 6)$ and $(5, -4)$. What is the equation of the line?
First, we can determine the slope with the equation:
$$ \begin{align} m = \frac{-4 - 6}{5 - -1}\\ = \frac{-10}{6}\\ = -\frac{5}{3} \end{align} $$We can now fill in some of the information for the equation:
$$ \begin{align} y = -\frac{5}{3}x + b \end{align} $$By substituting in one of our ordered pairs we can obtain the $y$-intercept.
$$ \begin{align} 6 = -\frac{5}{3}(-1) + b 6 - \frac{5}{3} = b b = \frac{13}{3} \end{align} $$Our final equation is:
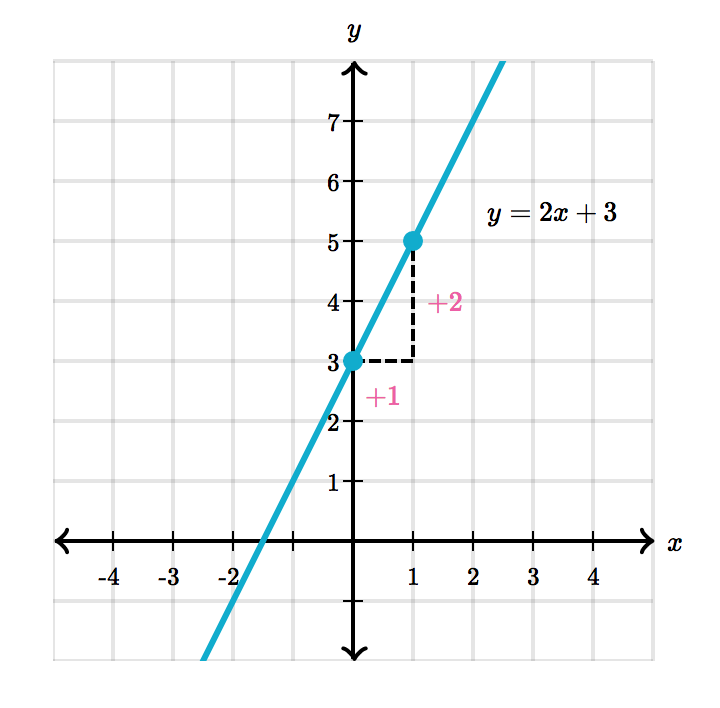
$$ \begin{align} y = -\frac{5}{3}x + \frac{13}{3} \end{align} $$Graph the equation $y = 2x + 3$.
First, we notice that the $y$-intercept is $(0, 3)$. We can obtain our next point by going up $2$ and over $1$:
Point-Slope Form
What is the linear equation (in point-slope form) whose solutions include $(4, 9)$ and $(6, 1)$?
We can immediately fill in our $a$ and $b$.
$$ \begin{align} y - 9 = m(x - 4) \end{align} $$Next, we can determine our slope with:
$$ \begin{align} m = \frac{1 - 9}{6 - 4}\\ = \frac{-8}{2}\\ = -4 \end{align} $$And, we can finish our equation:
$$ \begin{align} y - 9 = -4(x - 4) \end{align} $$Standard Form
Determine the $x$- and $y$-intercepts from the equation $9x + 16y = 72$.
We can determine the $x$-intercept by substituting in a $y$ value of $0$:
$$ \begin{align} 9x + 16(0) = 72\\ 9x = 72\\ x = \frac{72}{9}\\ x = 8 \end{align} $$We can determine our $y$-intercept by substituting in an $x$ value of $0$:
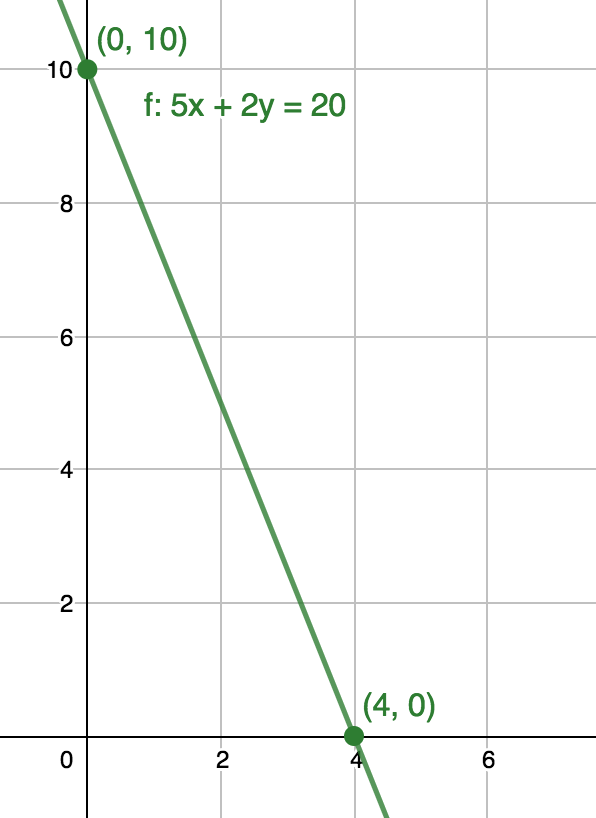
$$ \begin{align} 9(0) + 16y = 72\\ 16y = 72\\ y = \frac{72}{16}\\ y = \frac{9}{2} \end{align} $$Graph the equation $5x + 2y = 20$.
We can graph the line by determining the $x$- and $y$-intercepts:
$$ \begin{align} 5x + 2(0) = 20\\ 5x = 20\\ x = 4 \end{align} $$Our first point is the $x$-intercept of $(4, 0)$.
$$ \begin{align} 5(0) + 2y = 20\\ 2y = 20\\ y = 10 \end{align} $$Our second point is the $y$-intercept of $(0, 10)$.
We can plot the points and then draw the line for the equation:
Convert the following equation from point-slope form to standard form:
$$ \begin{align} y = \frac{3}{8}x + 5 \end{align} $$First, we want $x$ and $y$ on the same side…
$$ \begin{align} y - \frac{3}{8}x = 5 \end{align} $$We also want to get rid of the fraction:
$$ \begin{align} 8y - 3x = 40 \end{align} $$All Forms
A line passes through the points $(-3, 6)$, and $(6, 0)$. Find the equation of this line in point-slope form, slope-intercept form, and standard form.
We can first determine our slope:
$$ \begin{align} m = \frac{0 - 6}{6 - -3}\\ = \frac{-6}{9}\\ = -\frac{2}{3} \end{align} $$We can now write our equation in point-slope form:
$$ \begin{align} y - 6 = -\frac{2}{3}(x + 3) \end{align} $$We can now determine standard form by rearranging the equation:
$$ \begin{align} y = -\frac{2}{3}x - 2 + 6\\ y = -\frac{2}{3}x + 4\\ y + \frac{2}{3}x = 4\\ 3y + 2x = 12 \end{align} $$We can now easily determine the $y$-intercept:
$$ \begin{align} 3y + 2(0) = 12\\ 3y = 12\\ y = 4 \end{align} $$Now that we have the slope and the $y$-intercept, we can write the equation in slope-intercept form:
$$ \begin{align} y = -\frac{2}{3}x + 4 \end{align} $$Linear Equations
slope-intercept formula
$$ \begin{align} y = mx + b \end{align} $$where $m$ and $b$ are constants
Slope Formula
- calculate average change from one point to the next e.g. average velocity, etc.
- slope is rise over run or in change $y$ over change in $x$ or change in $y$ for each change in $x$
- slope measures both steepness and direction of a line
- a negative slope ($m < 0$) goes from the top left to the bottom right
- a positive slope ($m > 0$) rises from left to right
- when $m > 1$ the slope is steeper
- when $m < 1$ the slope is gentler
- a horizontal line has a slope of $0$ e.g. $y = 4$.
- a vertical line has an undefined slope e.g. $x = 2$.
- slope of a line perpendicular to a line with slope $\frac{\Delta y}{\Delta x}$ is $- \frac{\Delta x}{\Delta y}$
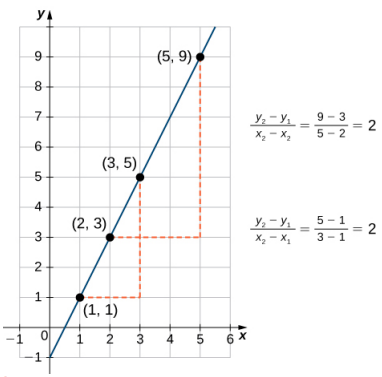
This ratio (slope) is independent of the points chosen:
We can treat $m$ as a coefficient $a$ instead, and quickly find the slope, if we do the following:
- Find $f(0)$
- This gives a point of $(0, b)$
- Now find $f(1)$
- This gives us $(1, a + b)$
- To find $a$ we can solve for $\frac{(a + b) - b}{1 - 0} = a$
Point-Slope Form
- Given $(x_1, y_1)$ and a slope of $m$ we can satisfy the equation:
Modifying the equation slightly gives us point-slope form:
$$ \begin{align} f(x) - y_1 = m(x - x_1) \end{align} $$Standard form of a line
The notation $ax + by = c$ where $a$ and $b$ are both non-zero coefficients on $x$ and $y$ can be used for all lines including vertical lines. This is derived from $by = -ax + c$
Intersection of Two Lines
Where intersection is at $(x_3, y_3)$
$$ \begin{align} y_1 = m_1 \cdot x_1 + b_1\\ y_2 = m_2 \cdot x_2 + b_2\\ y_3 = m_2 \cdot \left(\frac{y_1 + b_1}{m_1} \right) + b_2\\ x_3 = \frac{y_3 + b_1}{m_1} \end{align} $$
Distance Between Two Points
- find the length of the hypotenuse